What is an Isosceles Triangle?
Everything You Need to Know About Isosceles Triangles
When it comes to learning about triangles, there are a handful of different types of triangles with very specific characteristics that you will need to be familiar with—and one of the most important and most common are isosceles triangles.
In this short guide, we will tell you everything you need to know about isosceles triangles, including the isosceles triangle definition, so that you can easily an isosceles triangle and solve problems involving isosceles triangles.
So, if you need an answer to the question “what is an isosceles triangle?”, then you are in the right place! You can click here to see an instant answer or you can continue reading through this short guide for a more in-depth explanation of the features and characteristics of isosceles triangles.
You can also use the quick links below to jump to a particular section of this guide:
Let’s start with a super quick review of triangles and definitions.
What is a Triangle?
By definition, a triangle is a polygon with three sides, three corners, and three interior angles. While any three-sided polygon that satisfies this definition can be called a triangle, there are several types of triangles with specific characteristics.
Examples of different types of triangles include equilateral triangles, right triangles, and, of course, isosceles triangles.
All of the different types of triangles are shown in Figure 01 for your reference.
Figure 01: Types of Triangles
What is an Isosceles Triangle?
Isosceles Triangle Definition: An Isosceles Triangle is a triangle that has two sides of equal length.
Pretty simple, right?
By definition, an isosceles triangle is a triangle that has two sides of equal length.
Any triangle that has at least two sides of equal length can be considered an isosceles triangle.
In Figure 02 below, you can see three different examples of isosceles triangles. The notches on the sides indicate that they are equal in length to each other.
Figure 02: The isosceles triangle definition states that a triangle is isosceles when it has two equal sides.
What are the Properties of Isosceles Triangles?
Now that you know the basic definition of an isosceles triangle, let’s dive deeper into the properties of isosceles triangles and their sides and angles.
Key Properties of Isosceles Triangles
In addition to having two equal sides, the angles opposite of those two equal sides are also equal.
An altitude drawn from the base of an isosceles triangle to its vertex will always be perpendicular to that base and will dive the base into two congruent segments.
These key features are illustrated in Figure 03 below.
Figure 03: Properties of Right Triangles
Figure 03 above shows isosceles triangle △EFG. Notice that sides EF and EF are congruent (which makes this triangle isosceles by definition) and that ∠EFG and ∠EGF are also congruent.
Additionally, the altitude EH is perpendicular to the base segment FG, dividing FG into two congruent halves: segments FH and GH.
These properties apply to any isosceles triangle. If you understand these properties, you can apply them to any math problem involving an isosceles triangle!
Now that you know what is an isosceles triangle and the isosceles triangle definition, you are ready to learn about a special types of isosceles triangle—namely an isosceles right triangle (i.e. an isosceles triangle with one 90-degree angle).
What is an Isosceles Right Triangle?
An isosceles right triangle is a special type of isosceles triangle where the vertex angle is a right angle (i.e. it is equal to 90 degrees), and the two congruent angles are both equal to 45 degrees.
The isosceles right triangle is often referred to as a 45-45-90 right triangle in reference to the three angle measures being 45 degrees, 45 degrees, and 90 degrees.
These key characteristics of the isosceles right triangle are shown in Figure 04 below.
Figure 04: The properties of an isosceles right triangle.
We decided to conclude this guide by featuring the isosceles right triangle since its properties are so unique and the fact that the isosceles right triangle commonly shows up on math problems, so math students should be familiar with them.
Notice in Figure 04 above that the isosceles right triangle meets the definition of an isosceles triangle since it has two equal sides (sides AB and CB are congruent) and the angles opposite those sides are also congruent (∠BAC and ∠BCA are congruent).
However, in addition to meeting the criteria for being an isosceles triangle, an isosceles right triangle has a vertex angle that is equal to 90 degrees (i.e. it has one right angle) and the two congruent angles are both equal to 45 degrees, which is why the isosceles right triangle is often referred to as a 45-45-90 right triangle.
Conclusion: What is an Isosceles Triangle?
If you came to this guide wondering “what is an isosceles triangle?”, you now know the isosceles triangle definition as well as the key characteristics and properties of isosceles triangles.
Key Takeaway: A triangle is isosceles if it has two equal sides.
Beyond this basic isosceles triangle definition, we explored the properties and relationships between the sides and angles of isosceles triangles, namely that:
Every isosceles triangle has at least two equal sides.
The angles opposite the equal sides are also congruent to each other.
The altitude drawn from the base of an isosceles triangle to its vertex will always be perpendicular to that base and will dive the base into two congruent segments.
There are also a few special types of isosceles triangles, especially the isosceles right triangle (also known as the 45-45-90 triangle). The isosceles right triangle is a special case where the vertex of the triangle is a 90 degree angle and the two congruent angles are both equal to 45 degrees.
In conclusion, isosceles triangles are polygons with interesting symmetrical properties that give math students incredible opportunities to explore and learn two-dimensional figures and how they relate to real life.
More Free Resources You Will Love:
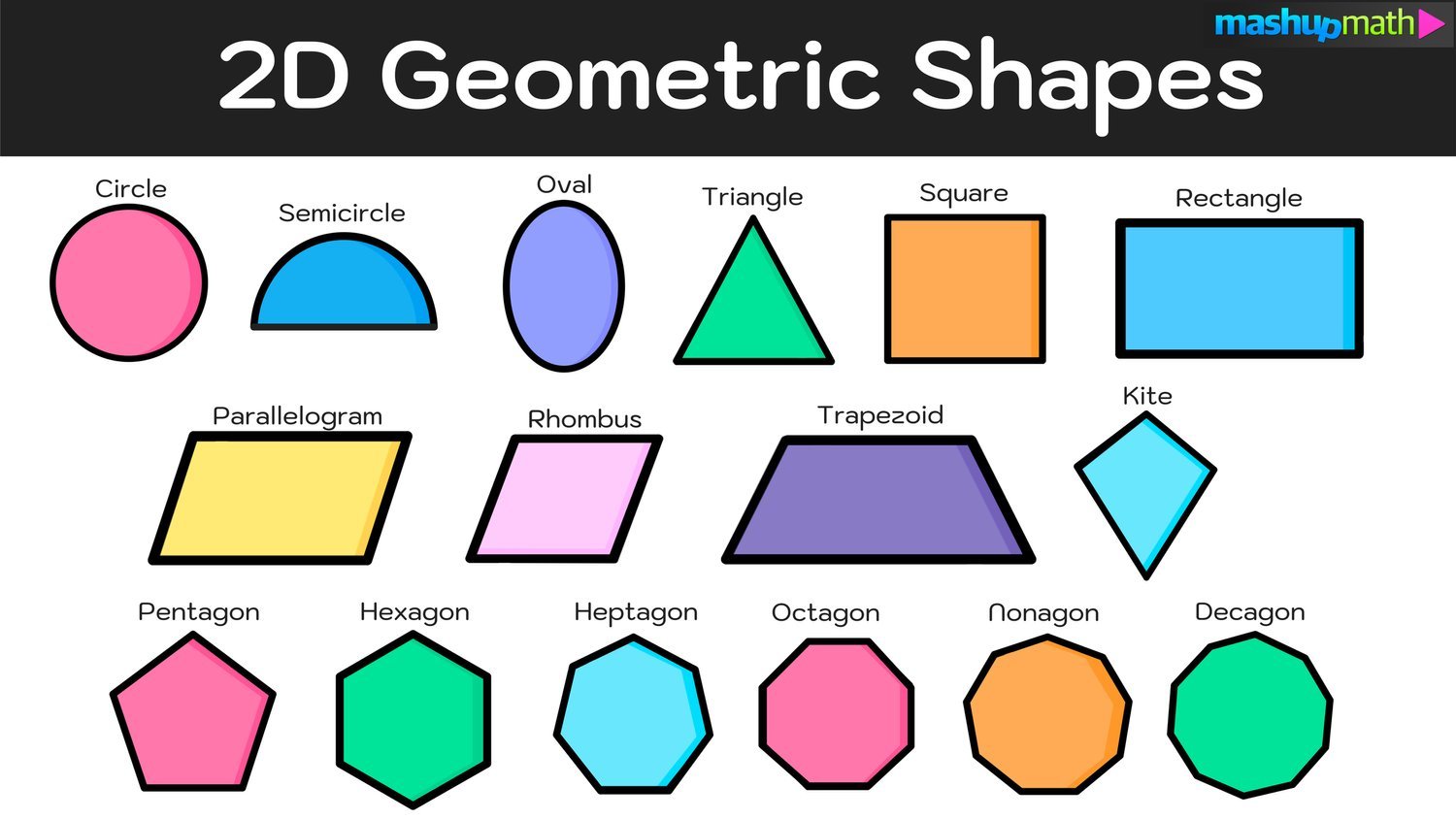
Geometric Shapes-Complete Guide
Everything you need to know about the properties and characteristics of every 2D geometric shapes.