Is 0 a Whole Number? Yes or No?

What is the definition of a whole number and is 0 a whole number?

When learning about the different categories of numbers (natural numbers, whole numbers, integers, etc.), zero can sometimes get lost in the shuffle. Many students often wonder: “Is 0 a whole number?” If you are asking this question yourself, you can click here for an instant answer or you can read through this short guide for a complete explanation, which includes definitions to some important math vocabulary terms related to numbers.

Before we determine whether or not 0 is a whole number, let’s do a quick review of the difference between natural numbers and whole number in math.

Natural Numbers

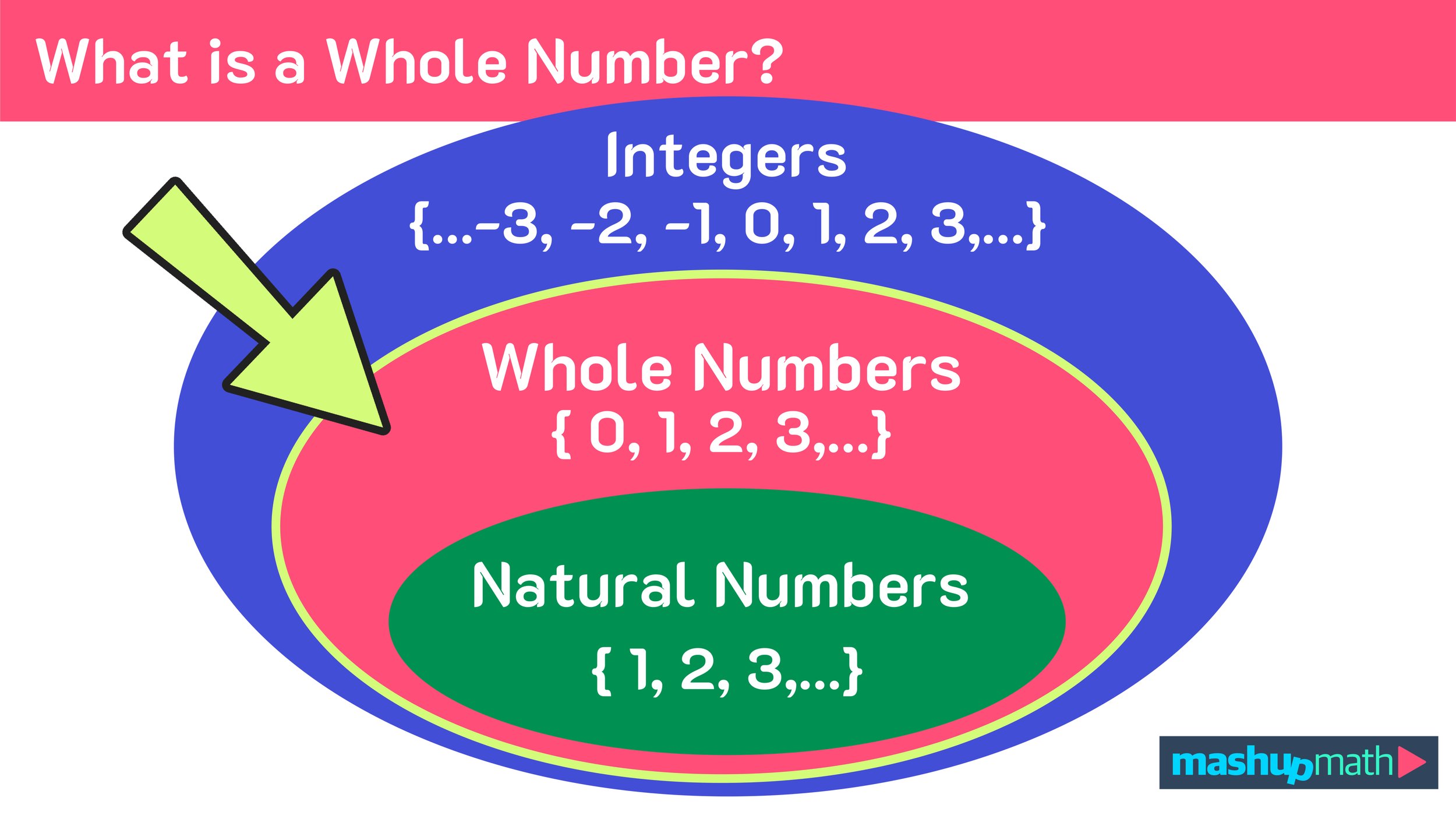
In math, a natural number is a number that can be used for counting or ordering values or amounts. The set of natural numbers starts at 1 and continues as follows: { 1, 2, 3, 4, 5, 6, 7, …}

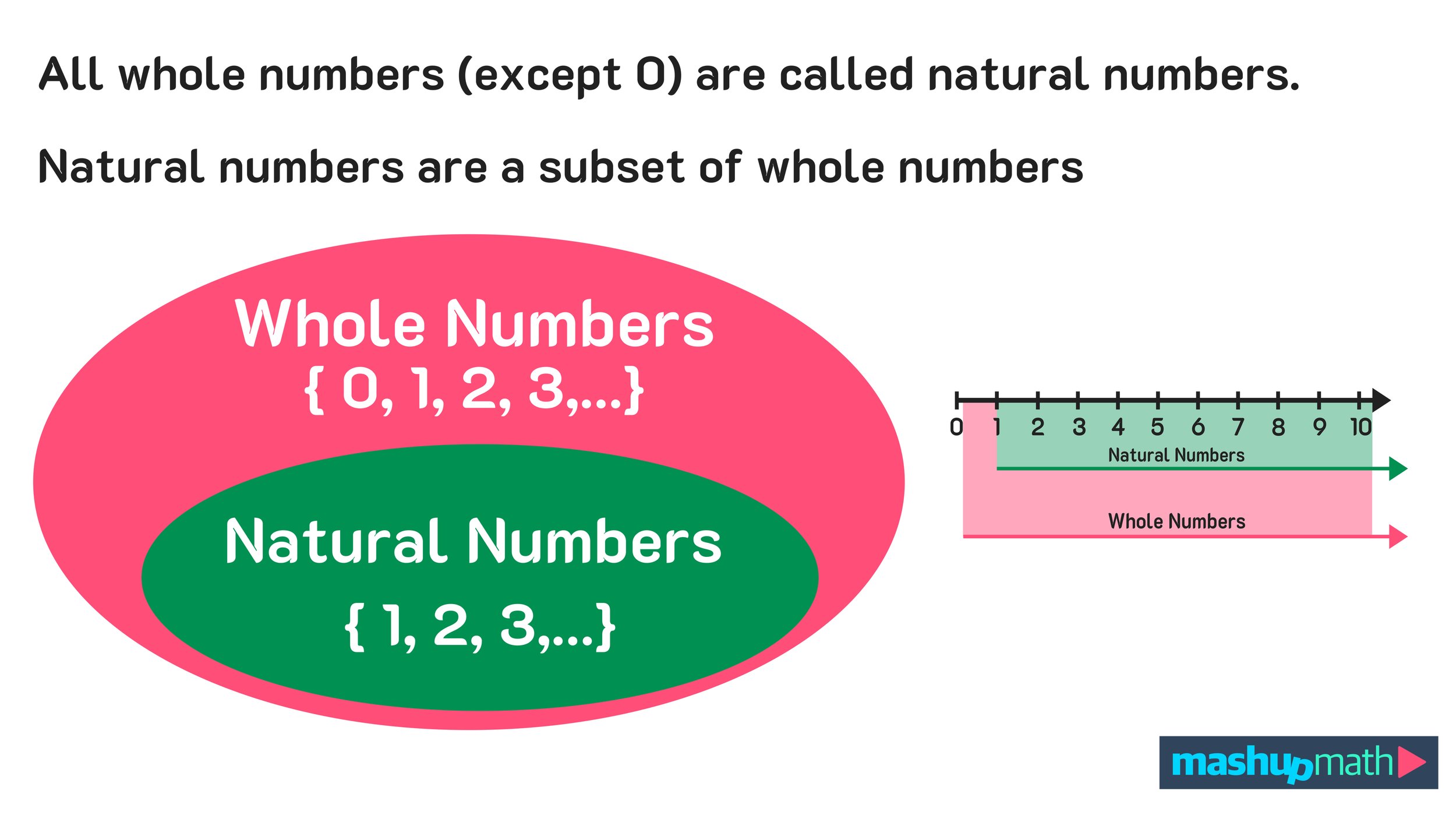
Notice that 0 is not included in this set and, thus, 0 is not a natural number.

Whole Numbers

In math, a whole number is any number that does not include fractions, decimals, or negatives. Another way to think about the set of whole numbers is a set that includes all of the positive integers as well as zero. The set of whole numbers starts at 0 and continues as follows: { 0, 1, 2, 3, 4, 5, 6, 7, …}

Notice that 0 is indeed included in this set and, thus, we can conclude that…

Is 0 a Whole Number?

Instant Answer: Zero is a Whole Number

Yes, zero is a whole number.

Why? By definition, 0 is not included in the set of natural numbers (i.e. zero is not a natural number), but it is included in the set of whole numbers (i.e. zero is a whole number).

Additionally, 0 is the first whole number and is followed by 1, 2, 3, 4, 5, etc.

The graphic in Figure 02 below shows how zero is included in the set of whole numbers but not in the set of natural numbers.

Zero's Important Place in the Number System

Why is zero such an important number when it comes to the universe of numbers? We have already established that, by definition, zero is a whole number. As far as values go, zero is unique because it represents the absence of value or a null quantity (i.e. zero represents nothing, which is why it is neither positive nor negative)

So, why is 0 a whole number? Because the concept of counting whole values relies on 0 to serve as a starting point (i.e. the point where you have nothing). Without this starting point, all non-zero whole numbers would lose their context.

If this explanation is hard to understand, we can think about zero’s role as a whole number from a practical standpoint. For example, if you were measuring the number of days that you visited the gym last year, you would rely on 0 to represent the instance where you never attended at all. Then, the remaining whole numbers could be used to determine how many times you actually attended. And since you can’t visit the gym negative times or a fraction/decimal of a time, the set of whole numbers would be used for this particular scenario.

More Key Facts About Zero

If you were surprised to find out that 0 is a whole number, then you may also be surprised by some other interesting and fundamental facts about zero.

Here are a few examples of some surprising facts about zero,

Zero is a whole number.

Is 0 a whole number? As previously stated, zero is, by definition, a whole number, meaning that it is included in the set of whole numbers {0, 1, 2, 3, 4, 5, …}

Zero is an integer.

Is 0 an integer? Since the set of integers includes all of the whole numbers and their negative counterparts, we can also say that zero is an integer as well.

Zero is neither negative nor positive.

Is 0 positive or negative? The set of integers includes every non-zero whole number and its negative counterpart as well as zero. This definition is worded this way because zero is the only integer that is neither negative nor positive. Zero is important in this sense because it is the “neutral value” that separates all of the positive numbers from the negative numbers.

Zero is an even number.

Is 0 even or odd? While you can’t divide a number by zero, you can divide zero by a number. By definition, a number is even if it can be divided by 2 without any remainder. Since 0/2 = 0, we can say that, by definition, zero is an even number (and that zero is not an odd number).

Conclusion: Is 0 a Whole Number?

If you find yourself wondering “Is 0 a Whole Number?”, then it’s important that you understand the mathematical definition of a whole number in the first place.

In math, a whole number is any number that does not include fractions, decimals, or negatives. And, since 0 does not include fractions or decimals and is not negative, we know that 0 is included in the set of whole number {0, 1, 2, 3, 4, 5, 6, 7, …}.

In short, the answer to the question “Is 0 a Whole Number?” is yes! By definition, zero is included in the set of whole numbers and it plays the important role of the absence of value or a null quantity. All of the non-zero whole numbers have a value that is determined based on its distance from zero on the number line. Pretty cool, right?

Additionally, while zero is not a natural number, it is all of the following:

zero is a whole number
zero is an integer
zero is neither positive nor negative
zero is an even number

Whether you came to this page looking for a simple yes or no answer or a deep exploration of the properties of 0, we hope that you leave here with a greater appreciation of 0 and its status in the universe of real numbers. As you continue to learn zero’s place in the number system, you will continue to gain a deeper understanding of mathematics and numbers in general.