How to Divide Fractions in 3 Easy Steps
Math Skills: How do you divide fractions by fractions, how do you divide fractions with whole numbers, and how to divide mixed fractions?
Free Step-by-Step Guide: How to Divide Fractions Step-by-Step Guide
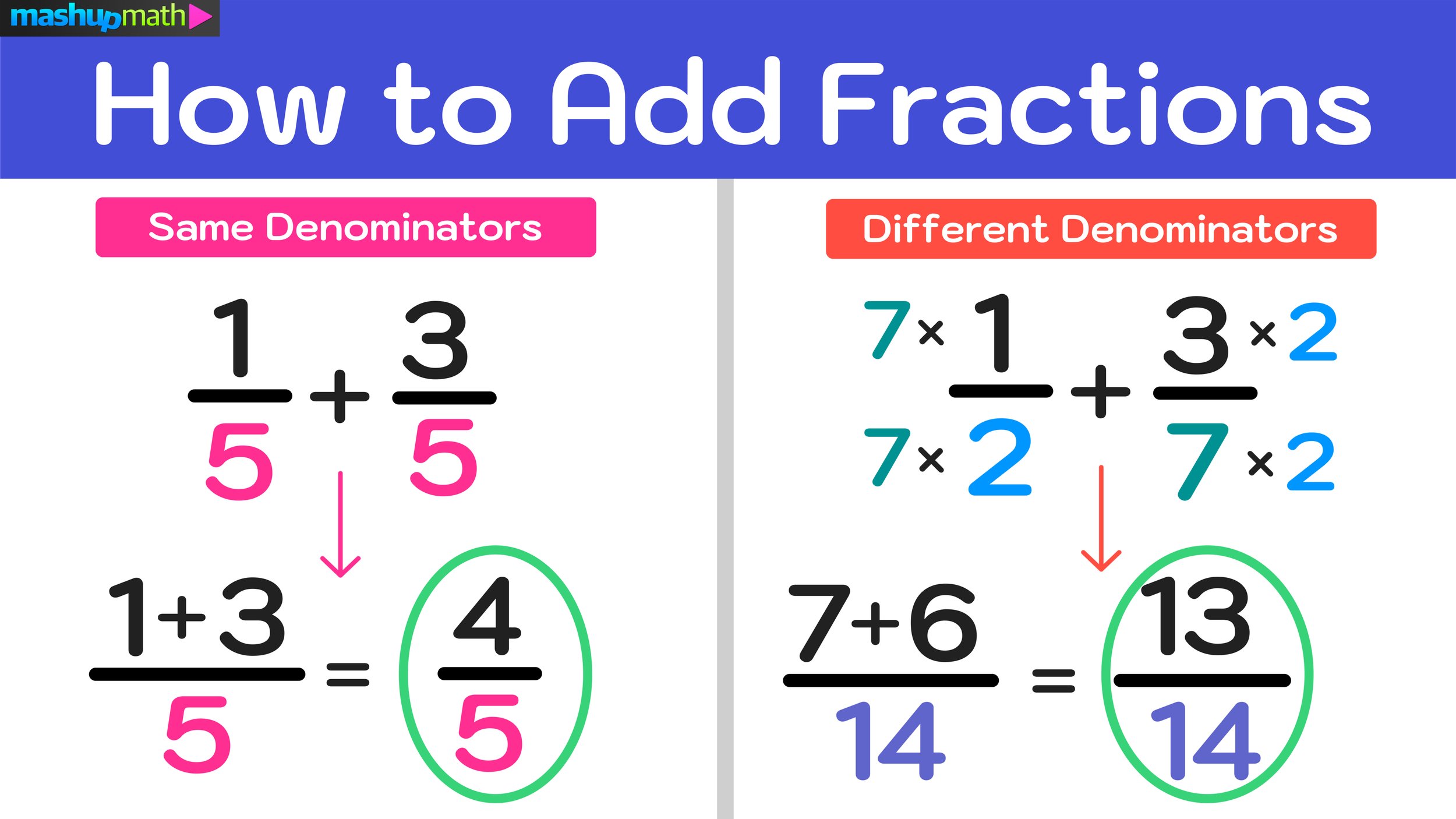
Performing operations on fractions can be challenging. Once you have mastered how to add fractions and how to subtract fractions, the next step is learning how to multiply and how to divide fractions.
The following free guide specifically focuses on teaching you how to divide fractions in the following scenarios:
While dividing fractions may seem challenging at first glance, you can actually easily solve all three types of problems by using a simple 3-step method for dividing fractions, which you will learn and apply to several practice problems further down in this step-by-step guide.
Together, we will learn the Keep-Change-Flip method for how to divide fractions and use it to solve a variety of practice problems.
However, before we dive into working through any examples, let’s do a quick review of some key vocabulary terms and prerequisite skills that you will need to refresh in order to be successful with this new math skill.
Before we cover how to subtract fractions and work through a few examples, let’s do a fast recap of some key characteristics and vocabulary terms related to subtracting fractions.
Are you ready to get started?
How to Divide Fractions: Key Vocabulary
Since we will be using several math vocabulary terms in this guide, it is important that you are familiar with their meanings before you start working on the practice problems.
What is the numerator of a fraction?
The numerator of a fraction is the top number of the fraction. For example, for the fraction 2/3, the numerator is 2.
What is the denominator of a fraction?
The denominator of a fraction is the bottom number of the fraction. For example, for the fraction 2/3, the numerator is 3.
Pretty simple, right? Whenever we mention the numerator of a fraction, we are talking about the top number. On the other hand, whenever we mention the denominator of a fraction, we are talking about the bottom number. Figure 01 below illustrates the relationship.
Figure 01: In any fraction, the numerator is the top number and the denominator is the bottom number.
Next, let’s make sure that you understand the difference between fractions, whole numbers, and mixed numbers (also referred to as mixed fractions).
What is a whole number?
In math, a whole number is a number that is not a fraction. For example, 7, 23, and 100 are all whole numbers.
What is a fraction?
In math, a fraction is a number that represents a part of a whole number. For example, 1/2, 2/3, and 5/8 are all fractions.
What is a mixed number?
In math, a mixed number (or a mixed fraction) is a number that consists of both a whole number and a proper fraction. For example, 3 2/5 is a mixed number that represents the sum of 3 and 2/5.
Why is it important for you to understand the key characteristics and differences between these three types of numbers? Because, in this guide, you will learn how to work with dividing each type of number using a simple 3-step method.
Figure 02: What is a whole number? What is a fraction? What is a mixed fraction?
Now that you are familiar with all of the key vocabulary related to how to divide fractions, you are ready to work through some practice problems. Let’s start with learning how to divide fractions by other fractions.
How to Divide Fractions by Fractions
How to Divide Fractions by Fractions: Example #1
Example #1: 1/4 ÷ 1/4
Our first dividing fractions example is very simple, and you may already know the answer. In this case, we are taking the fraction 1/4 (one-fourth) and dividing it by 1/4 (one-fourth). So, we are dividing the same non-zero value by itself, which we should already know will be equal to 1.
Even though we already know what the answer should be, let’s go ahead and learn our 3-step method for dividing fractions to this first practice problem to see if it works as it should.
How to Divide Fractions in 3 Easy Steps
Step One: Keep the first fraction as is.
Step Two: Change the division sign to a multiplication sign.
Step Three: Switch the position of the numerator and the denominator in the second fraction. Then multiply the numerators together and the denominators together and simplify if possible.
We will also be referring to this 3-step method as Keep-Change-Flip. Once you learn how to successfully follow these three simple steps, you can use them to solve any problem where you have to divide fractions!
Let’s go ahead and apply them to this first example: 1/4 ÷ 1/4
Step One: Keep the first fraction as is.
This first thing that you have to do is nothing at all. Simply leave the first fraction as is. So, 1/4 stays as 1/4.
Step Two: Change the division sign to a multiplication sign.
Next, take the division sign (÷) and change it to a multiplication sign (x) as follows:
1/4 ÷ → 1/4 x
Step Three: Switch the position of the numerator and the denominator in the second fraction. Then multiply the numerators together and the denominators together and simplify if possible.
For this last step, take the second fraction and “flip” the position of the numerator and the denominator. So, 1/4 becomes 4/1 as follows:
1/4 → 4/1
Now, we have used the Keep-Change-Flip method transform the original problem:
1/4 ÷ 1/4 → 1/4 x 4/1
Figure 03 below illustrates how we used the keep-change-flip method to transform the original division problem into a multiplication problem.
Figure 03: How to Divide Fractions: Transform the original division problem into a multiplication problem using keep-change-flip.
Finally, we can solve this problem by multiplying these two fractions together. To do this, simply multiply the numerators together and the denominators together as follows:
1/4 x 4/1 = (1x4) / (4x1) = 4/4 = 1
Final Answer: 1
When we multiply these two fractions together, we are left with (1x4) / (4x1) = 4/4 and we know that 4/4 can be reduced to 1, which we expected the answer to be when we first started this problem!
(Looking for some extra help with multiplying fractions, click here to access our free student guide).
Figure 04 below illustrates how we solved this problem after performing keep-change-flip on the original expression.
Figure 04: How to solve Example #1 after performing keep-change-flip on the original problem.
Confused? If so, that’s okay. The important thing is that you gain some experience with using keep-change-flip. Now let’s go ahead and apply it to another practice problem.
How to Divide Fractions by Fractions: Example #2
Example #2: 2/3 ÷ 4/5
For this second practice problem, we will again be using the 3-step method:
Step One: Keep the first fraction as is.
The first step, simply keep the first fraction 2/3 the same (i.e. you can just leave it as is).
Step Two: Change the division sign to a multiplication sign.
Next, take the division sign (÷) and change it to a multiplication sign (x) as follows:
2/3 ÷ → 2/3 x
Step Three: Switch the position of the numerator and the denominator in the second fraction. Then multiply the numerators together and the denominators together and simplify if possible.
Finally, flip the positions of the numerator and the denominator of the second fraction as follows:
4/5 → 5/4
Again, these 3-steps can be referred to as keep-change-flip, and they are illustrated below in Figure 05:
Figure 05: Transform the original problem from Example #2 using Keep-Change-Flip
As you can see, we have transformed the original problem using keep change flip and we can now solve it as follows:
2/3 x 5/4 = (2x5) / (3x4) = 10/12 = 5/6
Final Answer: 5/6
Remember, whenever you are multiplying two fractions together, you have to multiply the numerators together and then multiply the denominators together. In this example, we are left with (2x5)/(3x4) = 10/12, and, since 10 and 12 are both divisible by 2, we can reduce and express our final answer as 5/6.
Figure 06 below shows the complete process for solving this second example.
Figure 06: How to Divide Fractions Using the Keep-Change-Flip Method
Now, let’s go ahead and work through one more example of dividing a fraction by another fraction.
How to Divide Fractions by Fractions: Example #3
Example #2: 7/8 ÷ 11/12
Step One: Keep the first fraction as is.
As always, start by keeping the first fraction (7/8 in this example) as is.
Step Two: Change the division sign to a multiplication sign.
Next, change the division sign (÷) to a multiplication sign (x):
7/8 ÷ → 7/8 x
Step Three: Switch the position of the numerator and the denominator in the second fraction. Then multiply the numerators together and the denominators together and simplify if possible.
Now, flip the positions of the numerator and the denominator of the second fraction:
11/12 → 12/11
The keep-change-flip process for Example #3 is shown in Figure 07 below:
Figure 07: How to transform a fractions division problem using keep-change-flip.
Now that have transformed the original problem, we can solve it as follows:
7/8 x 12/11 = (7x12) / (8x11) = 84/88 = 21/22
Final Answer: 21/22
In this case, we end up with (7x12) / (8x11) = 84/88 and, since 84 and 88 are both divisible by 4, we can reduce and express our final answer as 21/22.
Figure 08 illustrates how we solved this problem.
Figure 08: How to Divide Fractions Using Keep-Change-Flip.
Next, we will learn how to divide fractions with whole numbers.
How to Divide Fractions with Whole Numbers
This next section will teach you how to divide a fraction by a whole number and how to divide a whole number by a fraction. We will again be using the keep-change-flip method to solve these kinds of problems. If you want a more in-depth review of how to use the keep-change-flip method, you can click here to revisit the previous section.
How to Divide a Fraction by a Whole Number: Example #1
Example #1: 3/7 ÷ 2
Ready for some good news? You can use the same keep-change-flip method from the previous section to solve these kinds of problems as well. However, there is one extra step involved. Whenever you want to divide a fraction by a whole number using keep-change-flip, you have to rewrite the whole number as a fraction by giving it a denominator of 1.
For this example, we can rewrite the whole number, 2, as a fraction as follows:
2 → 2/1
These both mean the same thing! Now, we can say that solving the original problem is the same as solving 3/7 ÷ 2/1. And since this new problem is just dividing a fraction by another fraction, we can use the keep-change-flip method as follows:
Step One: Keep the first fraction as is.
For the first step, simply keep the first fraction, 3/7, as is.
Step Two: Change the division sign to a multiplication sign.
For the second step, change the division sign (÷) into a multiplication sign (x) as follows:
3/7 ÷ → 3/7 x
Step Three: Switch the position of the numerator and the denominator in the second fraction. Then multiply the numerators together and the denominators together and simplify if possible.
Finally, flip the positions of the numerator and the denominator of the second fraction as follows:
2/1 → 1/2
The keep-change-flip process effectively transforms the division problem into an equivalent multiplication problem that is much easier to solve. This entire process is illustrated in Figure 09 below.
Figure 09: How to Divide a Fraction by a Whole Number: Rewrite the whole number as a fraction with a denominator of 1 and use the keep-change-flip method to solve.
Using the keep change flip method transforms the original division problem into an equivalent multiplication problem. To multiply two fractions together, simply multiply the numerators together and then multiply the denominators together as follows:
3/7 x 1/2 = (3x1) / (7x2) = 3/14
Notice that the result, 3/14, can not be reduced. Therefore:
Final Answer: 3/14
The graphic in Figure 10 below details the entire process for solving this problem.
Figure 10: 3/7 x 1/2 = 3/14
In the next example, we will use the exact same process to divide a whole number by a fraction.
How to Divide a Whole Number by a Fraction: Example #2
Example #1: 9 ÷ 3/4
If we want to use the keep-change-flip method to divide a whole number by a fraction, then we will have to rewrite the whole number (9 in this case) as a fraction as follows:
9 → 9/1
Now we can rewrite the original problem 9 ÷ 3/4 as 9/1 ÷ 3/4 (remember that these expressions are equivalent—i.e. they both mean the same thing). Now that we have two fractions being divided by each other, we can use keep-change-flip to solve.
Step One: Keep the first fraction as is.
Just like before, start by keeping the first fraction, 9/1, as is.
Step Two: Change the division sign to a multiplication sign.
Next, change the division sign (÷) into a multiplication sign (x) as follows:
9/1 ÷ → 9/1 x
Step Three: Switch the position of the numerator and the denominator in the second fraction. Then multiply the numerators together and the denominators together and simplify if possible.
Finally, flip the numerator and the denominator of the second fraction as follows:
3/4 → 4/3
The entire process of using keep-change-flip to transform this problem is illustrated in Figure 11 below.
Figure 11: How to Divide a Whole Number by a Fraction: Start by rewriting the whole number as a fraction and then use keep-change-flip to solve.
Now we can solve the problem by multiplying these two fractions together as follows:
9/1 x 4/3 = (9x4) / (1x3) = 36/3 = 12
Notice that the result, 36/3, can be reduced. Since both the numerator and denominator are divisible by 3, we can conclude that the final answer is 12/1 or just 12.
Final Answer: 12
The graphic in Figure 12 further illustrates how we solved this problem.
Figure 12: How to divide a whole number by a fraction using keep-change-flip
Now that you know how to divide a fraction by a whole number and how to divide a whole number by a fraction, let’s move onto the final section where you will learn how to divide mixed fractions.
How to Divide Mixed Fractions
The final section of the How to Divide Fractions guide will focus on how to divide mixed fractions and how to divide fractions with mixed numbers.
Again, we can solve all of these types of problems by using the keep-change-flip method (click here to revisit the previous section).
Let’s get started with our first example!
How to Divide Fractions with Mixed Numbers: Example #1
Example #1: 5/9 ÷ 3 1/3
Whenever you have to divide fractions with mixed numbers, you can use the keep-change-flip method to find the answer. However, before you can use keep-change-flip, you will have to convert the mixed number into an improper fraction first.
In this example, we have to convert the fraction 3 1/3 into an improper fraction (a fraction whose numerator is greater than its denominator).
We can rewrite 3 1/3 as 10/3 because:
3 1/3 = 3/3 + 3/3 + 3/3 + 1/3 = 10/3
If you need more help with converting mixed numbers into improper fractions, we highly recommend checking out this free guide before moving forward.
Now, we can rewrite the original problem as follows:
5/9 ÷ 3 1/3 → 5/9 ÷ 10/3
Both of these expressions are equivalent to each other. The key difference here is that the new expression allows us to use the keep-change-flip method to solve it as follows:
Step One: Keep the first fraction as is.
As always, simply keep the first fraction, 5/9, as is.
Step Two: Change the division sign to a multiplication sign.
Next, change the division sign (÷) to a multiplication sign (x) as follows:
5/9 ÷ → 5/9 x
Step Three: Switch the position of the numerator and the denominator in the second fraction. Then multiply the numerators together and the denominators together and simplify if possible.
Lastly, flip the positions of the numerator and the denominator of the second fraction as follows:
10/3 → 3/10
Why are we doing this? Remember that the keep-change-flip method allows us to transform the original division problem into an equivalent multiplication problem that will be much easier to solve. This process is highlighted in Figure 13 below.
Figure 13: How to Divide Fractions with Mixed Numbers: Rewrite the mixed number as an improper fraction and then use keep-change-flip to solve.
From here, we can solve by multiplying these two fractions together as follows:
5/9 x 3/10 = (5x3) / (9x10) = 15/90 = 1/6
Final Answer: 1/6
Figure 14 below illustrates how we were able to divide fractions with mixed numbers and solve this problem.
Figure 14: How to Divide Fractions with Mixed Numbers Explained
Now, let’s work through the final example of this guide where you will learn how to divide mixed fractions.
How to Divide Mixed Fractions: Example #2
Example #1: 6 1/2 ÷ 2 1/4
Just like the previous example, we can use the keep-change-flip method to solve this problem, but first we have to convert the mixed fractions in this problem into improper fractions.
In this case:
6 1/2 = 2/2 + 2/2 + 2/2 + 2/2 + 2/2 + 2/2 + 1/2 = 13/2
2 1/4 = 4/4 + 4/4 + 1/4 = 9/4
So, we can rewrite the original problem as:
6 1/2 ÷ 2 1/4 → 13/2 ÷ 9/4
Figure 14: How to Divide Mixed Fractions: Start by rewriting any mixed fractions as improper fractions.
Again, if you need to review how to convert a mixed numbers into an improper fraction, we highly recommend checking out this free step-by-step guide.
Now, we have a new, yet equivalent, expression to be solved using keep-change-flip:
13/2 ÷ 9/4
Step One: Keep the first fraction as is.
First, keep the first fraction, 13/2, as is.
Step Two: Change the division sign to a multiplication sign.
Second, change the division sign (÷) to a multiplication sign (x) as follows:
13/2 ÷ → 13/2 x
Step Three: Switch the position of the numerator and the denominator in the second fraction. Then multiply the numerators together and the denominators together and simplify if possible.
And finally, flip the numerator and the denominator positions of the second fraction:
9/4 → 4/9
Figure 15: How to Divide Mixed Fractions Explained
The last thing we have to do to solve this problem is multiply these two improper fractions together as follows:
13/2 x 4/9 = (13x4) / (2x9) = 26/9 or 2 8/9
For this example, we are left we the improper fraction 26/9, which can not be reduced any further. You can also convert 26/9 into a mixed number, which would be 2 8/9. Both of these answers are equivalent.
Final Answer: 26/9 or 2 8/9
Figure 16 below shows how we found this final answer.
Figure 16: You will likely have to convert your final answer into a mixed number.
Conclusion: How to Divide Fractions
Dividing fractions can be a conceptually challenging math task, but learning how to use the keep-change-flip method can make the process much easier.
Whether you are dividing fractions with other fractions, fractions with whole numbers, whole numbers with fractions, or fractions with mixed numbers, the keep-change-flip method provides a simple three-step process for solving these types of problems.
The keep-change-flip method for dividing fractions can be summarized as follows:
Step One: Keep the first fraction as is.
Step Two: Change the division sign to a multiplication sign.
Step Three: Flip the position of the numerator and the denominator in the second fraction.
After you perform keep-change-flip, you can solve the problem by multiplying and reducing the result whenever possible.
Search Tags: how to subtract fractions, subtracting fractions, how to subtract fractions with different denominators, fraction subtraction, subtracting fractions with unlike denominators, how do you subtract fractions?