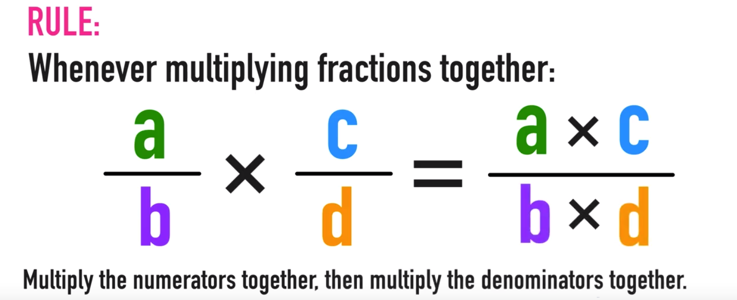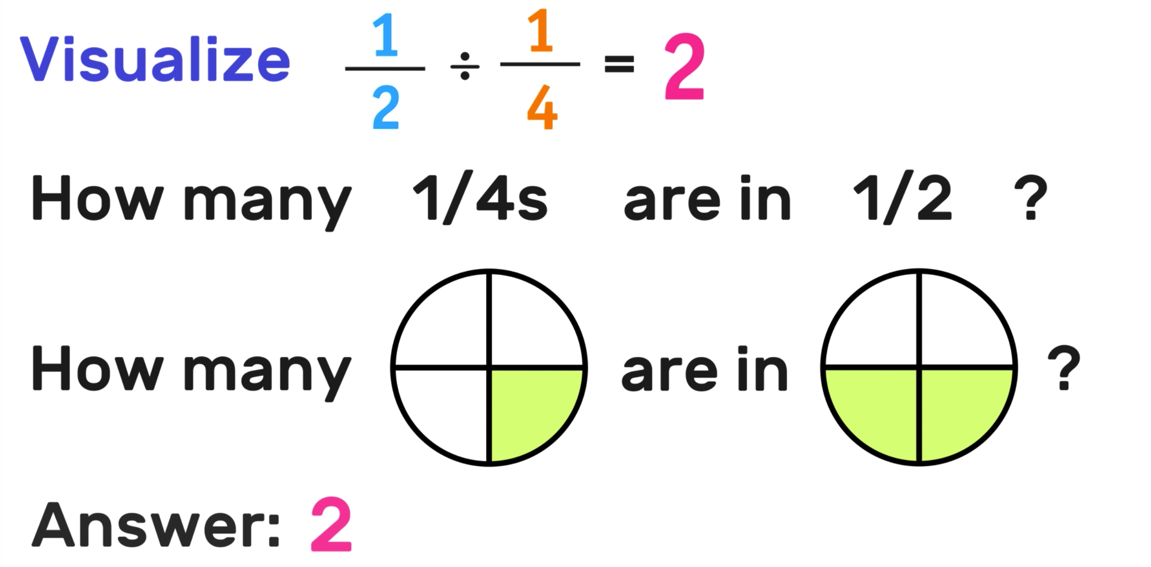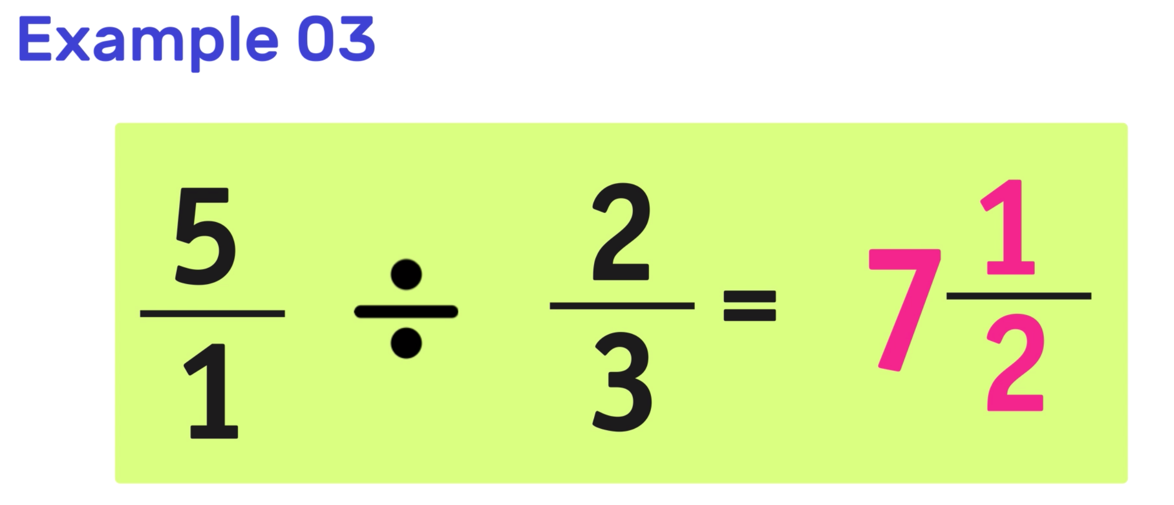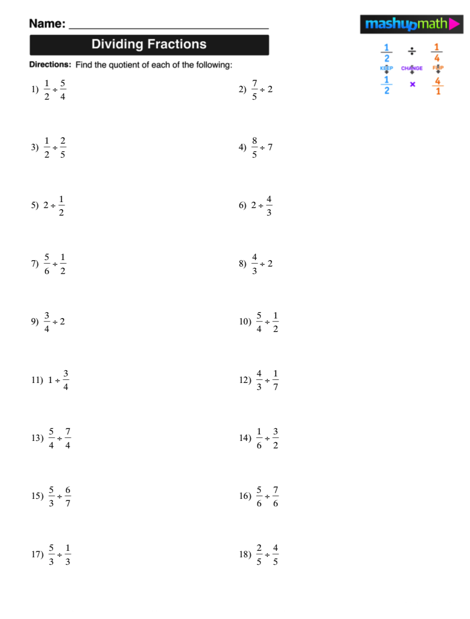Complete Guide: Dividing Fractions

Key Question: How do you divide fractions by fractions and fractions with whole numbers?

Welcome to this free step-by-step guide to dividing fractions. This guide will teach you how to use a simple three-step method called Keep-Change-Flip to easily divide fractions by fractions (and fractions by whole numbers as well).

Below you will find several examples of how to divide fractions using the Keep-Change-Flip method along with an explanation of why the method works for any math problem that involves dividing fractions. Additionally, this free guide includes an animated video lesson and a free practice worksheet with answers!

Are you ready to get started?

Dividing Fractions: Multiplication Review

Before you learn how to divide fractions using the Keep-Change-Flip method, you need to make sure that you understand how to multiply fractions together (which is even easier than dividing!).

Since multiplying fractions is typically taught before dividing fractions, you may already know how to multiply two fractions together. If this is the case, you can skip ahead to the next section.

However, if you want a quick review of how to multiply fractions, here is the rule:

Multiplying Fractions Rule: Whenever multiplying fractions together, multiply the numerators together, then multiply the denominators together as follows…

For example, 3/4 x 1/2 can be solved as follows:

Looking for More Help with Multiplying a Fraction by a Fraction? Check out this free guide

Dividing Fractions Examples!

Now that you know how to multiply fractions, you are ready to learn how to divide fractions using the simple 3-step Keep-Change-Flip method.

Let’s start with a simple example

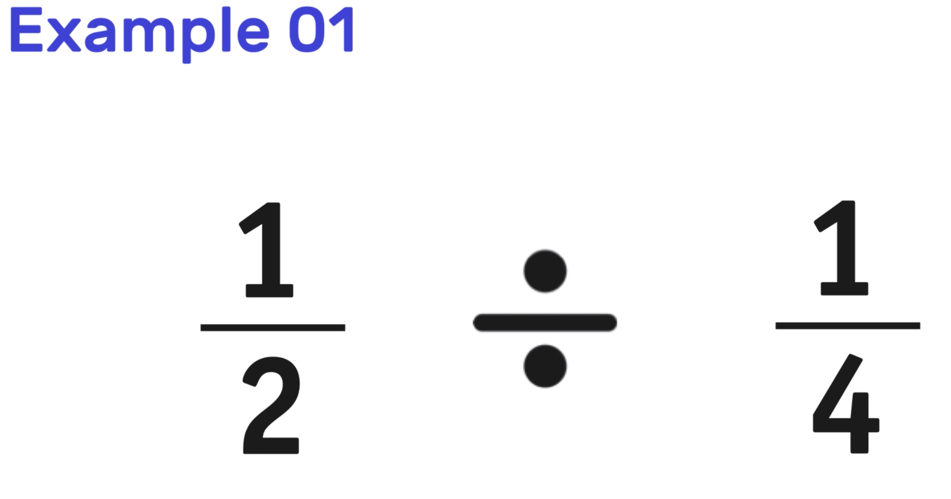
Dividing Fractions Example 1

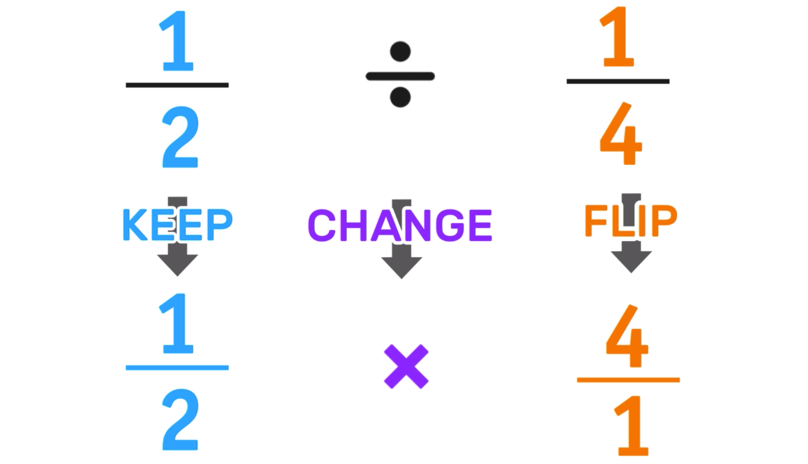
Example 1: What is 1/2 ÷ 1/4 ?

To solve this example (and any problem where you have to divide fractions, we are going to use the Keep-Change-Flip method)

Where:

1.) KEEP = Keep the first fraction as is and just leave it alone.

2.) CHANGE = Change the division sign to a multiplication sign.

3.) FLIP = Flip the second fraction (swap the numerator and the denominator)

These steps can be applied to example 1 as follows:

Again, after applying Keep-Change-Flip, we have transformed the original problem of 1/2 ÷ 1/4 as follows:

Now you can solve the problem by multiplying the fractions together and simplifying if necessary:

The final answer is 2, and we can conclude that the answer to the original problem is…

Final Answer: 1/2 ÷ 1/4 = 2

Why Does This Answer Mean?

In example 1, we concluded that 1/2 ÷ 1/4 = 2. But what does this actually mean?

If we think about 1/2 ÷ 1/4 in the form of a question: How many 1/4s are in 1/2?

And then if we visualize 1/4 and 1/2, we can clearly see that there are 2 1/4s in 1/2, which is why the final answer is 2.

Fraction Divided by Fraction: Example 2

Example 2: What is 2/9 ÷ 1/3 ?

Just like example 01, you can solve this problem by using the keep change flip method as follows:

1.) Keep the first fraction 2/9 as is.

2.) Change the division sign to multiplication.

3.) Flip the second fraction to turn 1/3 into 3/1

Next, perform 2/9 x 3/1 as follows and simplify the answer if you can:

In this example, 6/9 is not the final answer, since it can be reduced to 2/3

The final answer is 2/3, and we can conclude that the answer to the original problem is…

Final Answer: 2/9 ÷ 1/3 = 2/3

Dividing Fractions by Whole Numbers: Example 3

What if you have to divide a fraction with a whole number? It turns out the process is exactly the same as the previous examples!

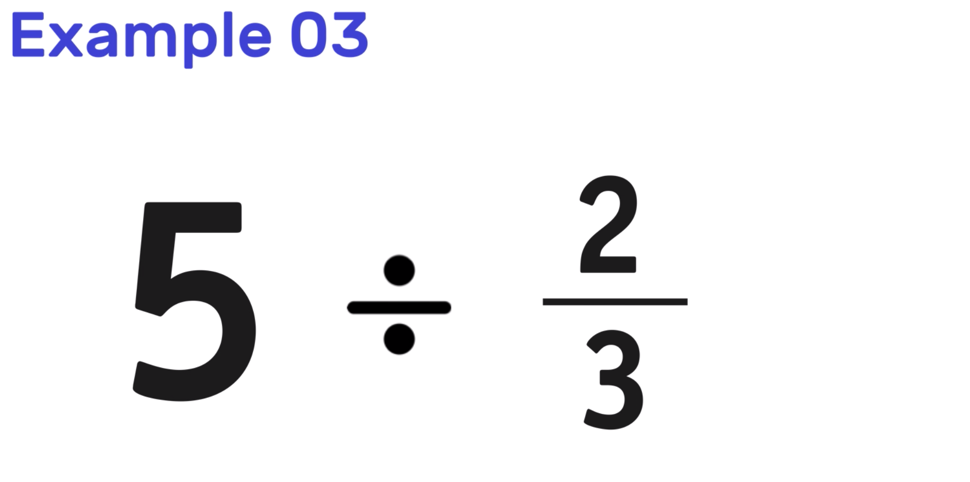
Example 03: What is 5 ÷ 2/3 ?

Notice that, in this example, you are dividing a fraction with a whole number. But it is actually very easy to convert a whole number into a fraction. All that you have to do is rewrite the number as fraction where the number itself is in the numerator and the denominator is 1.

For example, 5 can be rewritten as 5/1 and this rule applies for any whole number!

Now that you have rewritten the whole number as a fraction, you can use the Keep-Change-Flip method to solve the problem.

1.) Keep the first fraction 5/1 as is.

2.) Change the division sign to multiplication.

3.) Flip the second fraction to turn 2/3 into 3/2

Finally, multiply the fractions together and simplify if possible to find the final answer as follows:

In this example, the answer can be expressed as 15/2 or as 7 & 1/2.

And you can conclude that the answer to the original problem is…

Final Answer: 5 ÷ 2/3 = 15/2 or 7&1/2

Still confused? Check out the animated video lesson below:

Video: Dividing Fractions Explained!

Check out the video lesson below to learn more about how to divide fractions by fractions and fractions by whole numbers:

Dividing Fractions Worksheet

Are you looking for some extra practice dividing fractions? Click the links below to download your free worksheets and answer key:

CLICK HERE TO DOWNLOAD YOUR FREE WORKSHEET

Tags:  divide fractions, dividing fractions by whole numbers, dividing fractions examples, fraction divided by fraction

Keep Learning:

Have thoughts? Share your thoughts in the comments section below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

By Anthony Persico

Anthony is the content crafter and head educator for YouTube's MashUp Math. You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.