Converting Improper Fractions to Mixed Numbers: Your Complete Guide
How can you convert an improper fraction to a mixed number?
Welcome to this free lesson guide that accompanies this Converting Improper Fractions to Mixed Numbers video lesson, where you will learn the answers to the following key questions:
What is a mixed number?
What is a proper fraction?
What is an improper fraction?
What is the difference between a proper fraction and an improper fraction?
How do you convert improper fractions to mixed numbers?
This Converting Improper Fractions to Mixed Numbers: Complete Guide includes several examples, a step-by-step tutorial, an animated video mini-lesson, and a free worksheet and answer key.
*This lesson guide accompanies our animated Converting Improper Fractions to Mixed Numbers Tutorial on YouTube.
Want more free math lesson guides and videos? Subscribe to our channel for free!
Before you learn to convert improper fractions to mixed numbers you need to understand some key vocabulary first.
What is a Mixed Number?
A mixed number is a number consisting of an integer, like 3, and a proper fraction, like (2/5), as seen in the example below:
Figure 1
Note that a mixed number is ALSO equal to the sum of the integer and the fraction. The numbers shown in Figure 1 and Figure 2 both represent the same mixed number. The plus sign is not usually included, however, understanding this relationship will help you later on!
Figure 2
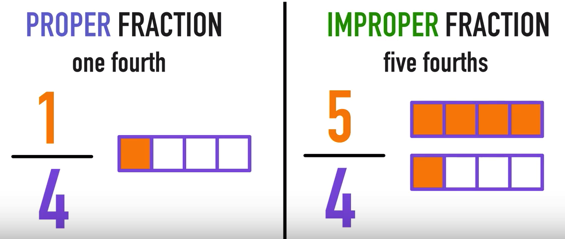
What is a Proper Fraction and What is an Improper Fraction?
What is the difference between a proper fraction and an improper fraction?
A proper fraction is a fraction where the value of the numerator is less than the value of the denominator.
The value of a proper fraction is less than one. For example, (1/4) or one fourth is a proper fraction.
An improper fraction is a fraction where the value of the numerator is greater than the value of the denominator.
The value of a proper fraction is greater than one. For example, (5/4) or five fourths is an improper fraction.
Notice that the value of an improper fractions is greater than one!
Now you’re ready to start converting improper fractions to mixed numbers, starting with the above example of (5/4).
How To Convert Improper Fractions to Mixed Numbers
Converting Improper Fractions to Mixed Numbers Example 1
Example 1: Convert five fourths into a mixed number
Let’s start by expressing (5/4) or five fourths as the sum of 5 one fourths as follows:
Since (1/4) is equal to one quarter, we can think about this example in terms of money and replace each (1/4) with one-quarter coins as follows:
And since four quarters equals one whole dollar…
In terms of money, five quarters equals one whole dollar and one quarter.
In terms of values, five quarters (or five fourths) equals one whole and one quarter. (or one fourth)
Answer:
(5/4) expressed as a mixed number…
You can think about this situation in a more visual way by observing Figure 3 below. You will use this kind of thinking to solve future problems involving converting improper fractions to mixed numbers!
Converting Improper Fractions to Mixed Numbers Example 2
Example 2: Convert thirteen sixths into a mixed number.
*Start by noting that 13 divided by 6 is equal to 2 with a remainder of 1, or 2R1.
Keep this fact in mind for now, as we’ll come back to it later!
(13/6) equals two with a remainder of 1
Next, let’s visualize what (13/6) looks like using fraction charts:
By combining these values (finding the sum): 1 + 1 + (1/6), we are left with a mixed number.
Answer:
(13/6) expressed as a mixed number…
This should make sense considering that we knew that 13 divided by 6 equaled 2 with a remainder of 1.
In this case, two wholes (six sixths) with a remainder of one sixth as shown in Figure 4 below.
Figure 4
Converting Improper Fractions to Mixed Numbers: Video Tutorial
Still confused? Check out the animated video lesson below:
Check out the video lesson below to learn more about converting improper fractions to mixed numbers and for more free practice problems:
Extra Practice: Free Converting Improper Fractions to Mixed Numbers Worksheet
Free Worksheet!
Are you looking for some extra practice? Click the links below to download your free worksheets and answer key:
Practice Converting Improper Fractions to Mixed Numbers:
Keep Learning with More Free Lesson Guides:
Have thoughts? Share your thoughts in the comments section below!
(Never miss a Mashup Math blog--click here to get our weekly newsletter!)
By Anthony Persico
Anthony is the content crafter and head educator for YouTube's MashUp Math. You can often find me happily developing animated math lessons to share on my YouTube channel . Or spending way too much time at the gym or playing on my phone.