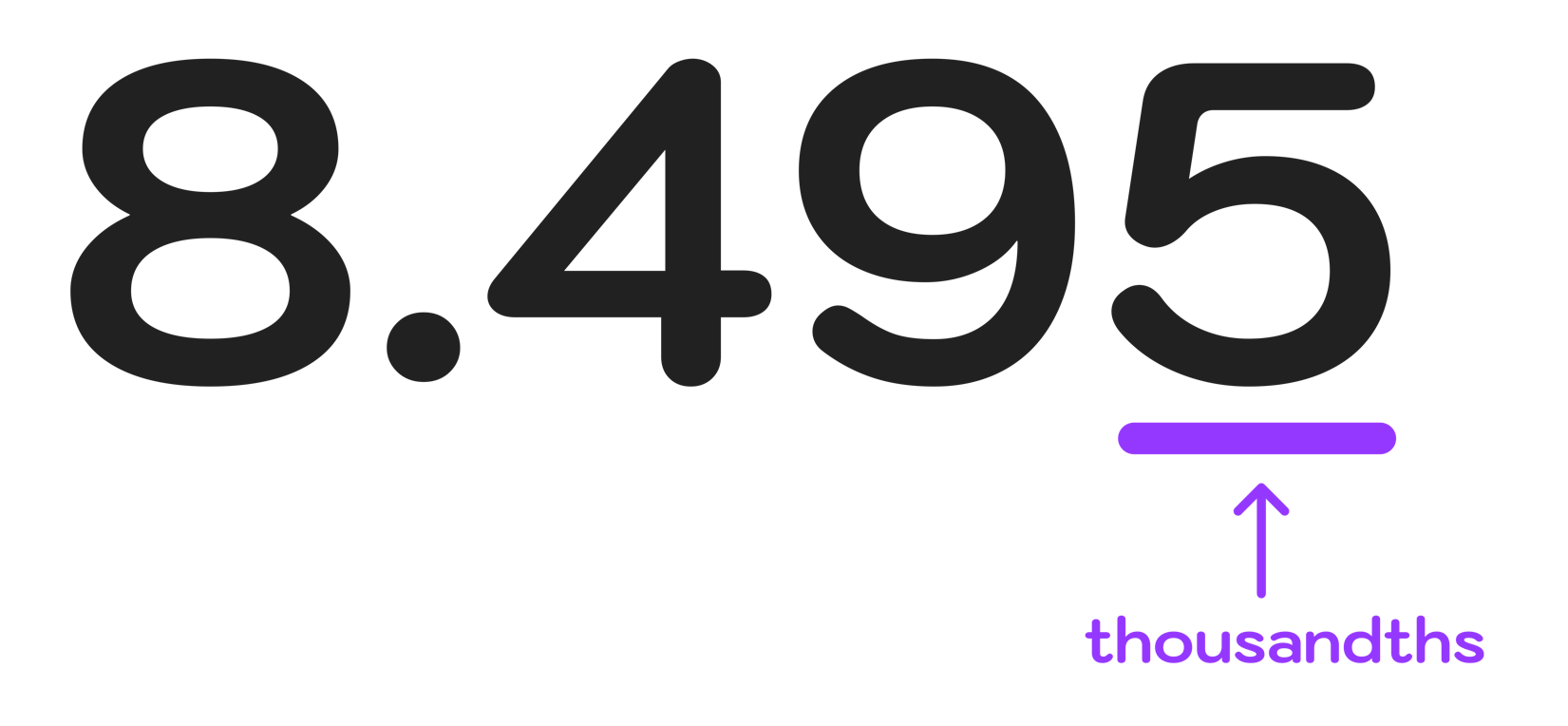Viewing entries tagged
how to factor a cubic polynomial

How to Round to the Nearest Hundredth—Step-by-Step Guide

Comment

How to Round to the Nearest Hundredth—Step-by-Step Guide

How to Round to the Nearest Hundredth

Step-by-Step Guide: Rounding to the Nearest Hundredth in 3 Easy Steps

 

Free Step-by-Step Guide: How to round to the nearest hundredth.

 

Knowing how to round numbers, especially numbers involving decimals, is an incredibly useful math skill that will help you to work large and small numbers and estimate their values.

While rounding whole numbers can be relatively straightforward, the process gets a little trickier when decimals are involved. However, this guide will make sure that you are familiar with key vocabulary and our easy-to-follow three-step method for rounding numbers to the nearest hundredth. Once you learn to apply this method, you can use it to solve any problem where you are tasked with rounding to the nearest hundredth.

Are you ready to get started? The following free guide will teach you everything you need to know about rounding to the nearest hundredth including step-by-step explanations of solving several practice problems.

While we highly recommend that you read each section in order, you can use the quick links below to jump to a specific topic or section:

(Looking for help with rounding to the nearest tenth and rounding to the nearest thousandth?)

What does rounding a number mean?

Rounding a number is the process of rewriting a number to a value that closely estimates its actual value so that is easier to understand and perform operations on.

For example, if a large coffee costs $4.97, you could estimate the cost to be $5 even (this would be an example of rounding to the nearest whole number). If someone asked you how much money you would need to purchase six coffees, you could easily estimate the cost to be $30 (since 5 x 6 =30), rather than having to figure out the value of 4.97 x 6.

So, rounding is just a method of making larger or small numbers easier to work with.

 

Figure 01: An example of rounding is estimating that the cost of a $4.97 cup of coffee to be $5 since it is an easier number to work with.

 

When do you round down and when do you round up?

Now that you understand what rounding means, it is important that you know the difference between situations when you have to round up and when you have to round down.

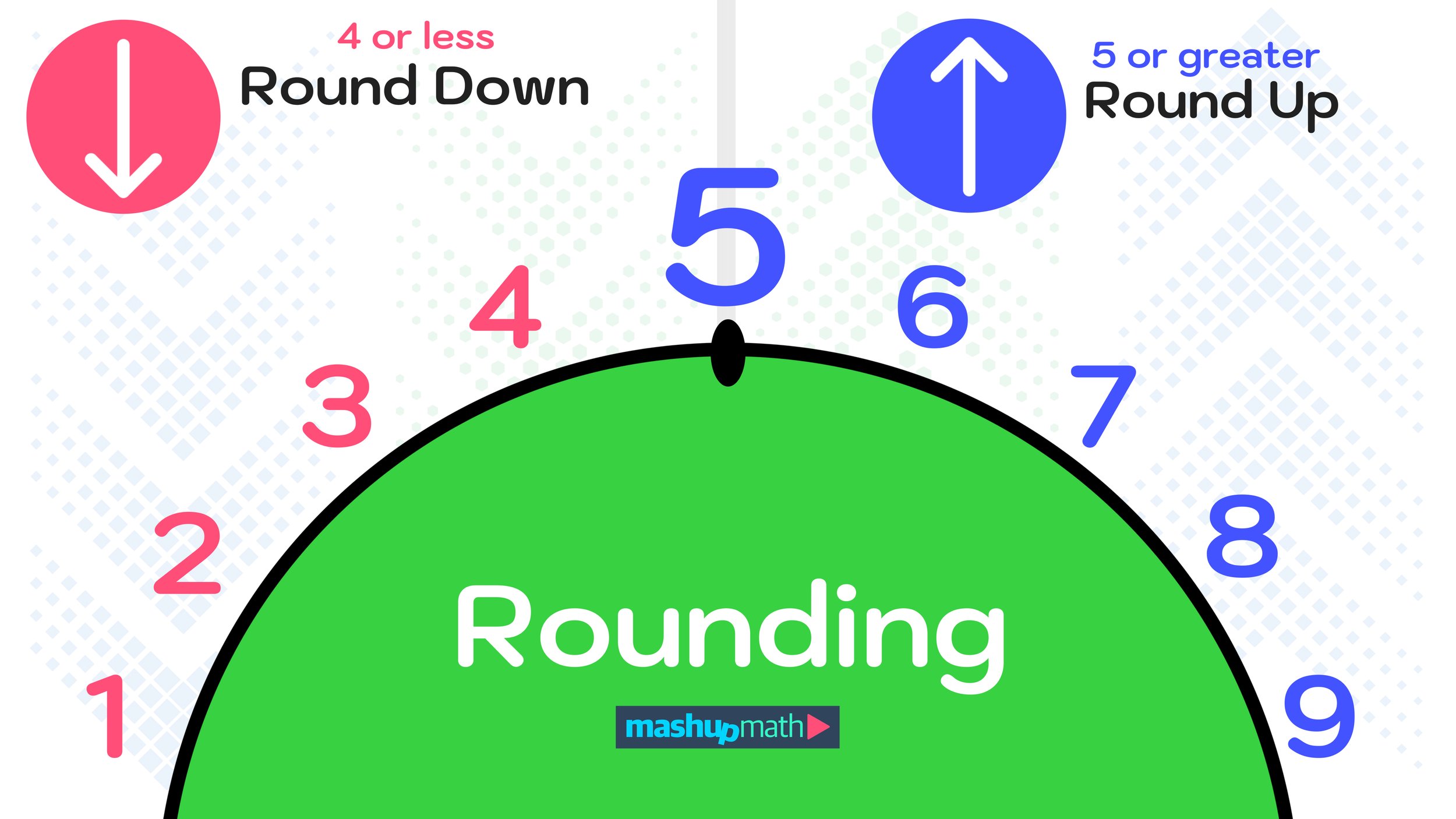
In the case of rounding, the number 5 is extremely significant.

RULE: If the number to the right of the number you are rounding is 5 or greater, then you must round up. If the number to the right of the number you are rounding is 4 or less, then you must round down.

This rule applies to rounding any whole number or decimal number. To help you to remember this rule, you can use the “rounding hill” shown in Figure 02 below to help you remember when to round up and when to round down.

  • If digit to the right of the number being rounded is 4 or less → round down

  • If digit to the right of the number being rounded is 5 or greater → round up

For example, if you wanted to round 58 to the nearest ten, the rounded answer is 60 since 8 (the number to the right of the tens digit) is 5 or greater, meaning you have to round up.

  • 58 → 8 is 5 or greater, so round up → 60

On the other hand, if you wanted to round 43 to the nearest ten, the result would be 40 since 3 (the number to the right of the tens digit) is 4 or less, meaning you have to round down.

  • 43 → 3 is 4 or less, so round down → 40

 

Figure 02: This illustration of a “rounding hill” can help you to remember when to round up and when to round down.

 

What does rounding to the nearest hundredth mean in terms of place value?

The last key topic that we have to review before we start working on some examples of rounding to the nearest hundredth is place value.

Definition: Place Value is the numerical value that a digit has based on its position in the number.

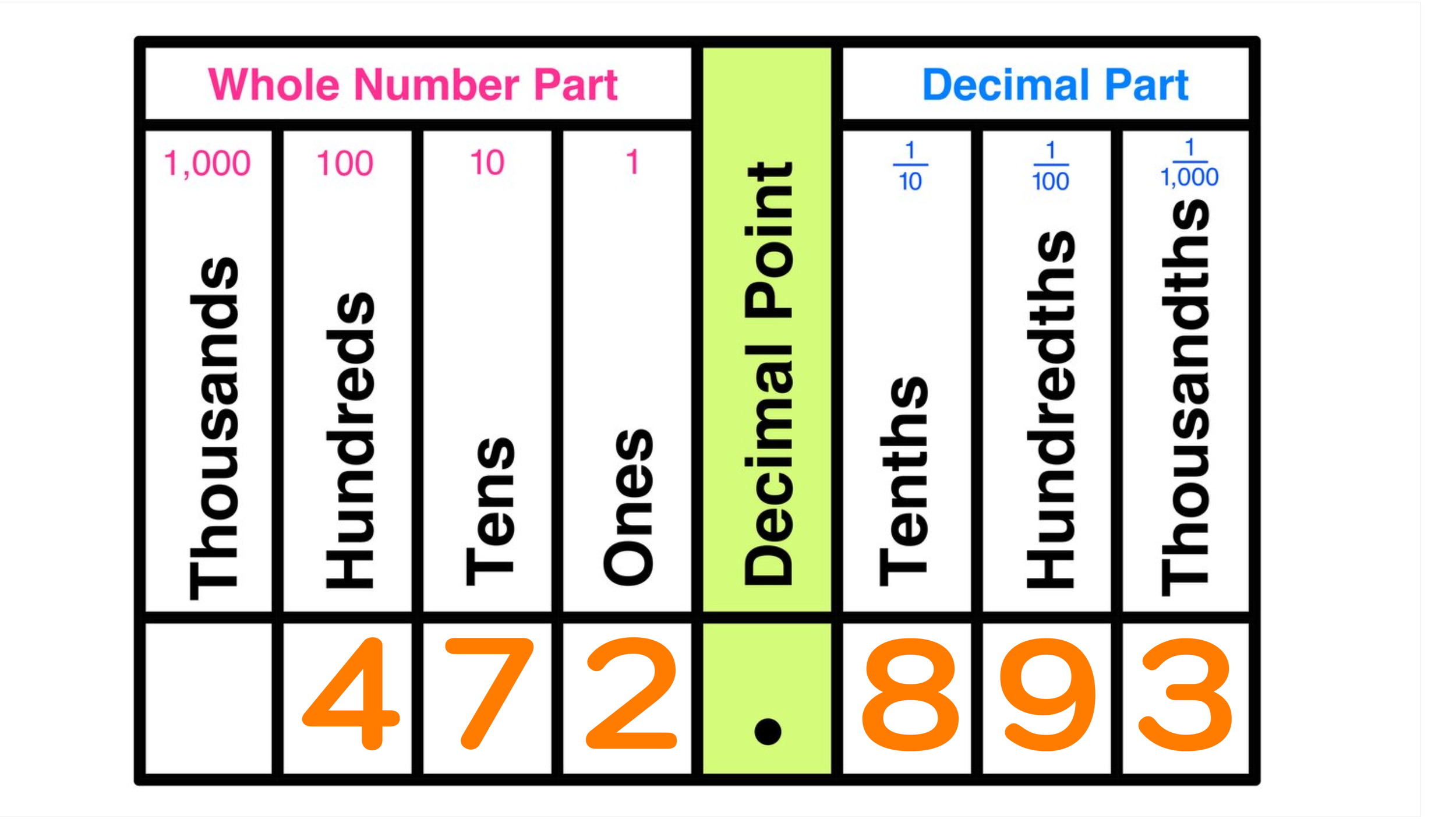
Consider the number 472.893

We can think of the number 472.893 as the sum of:

  • 4 hundreds

  • 7 tens

  • 2 ones

  • 8 tenths

  • 9 hundredths

  • 3 thousandths

Just like the “rounding hill” in Figure 02, you can use a place value chart, as shown in Figure 03 below, as a visual tool to help you to correctly identify the place values of digits in any given number.

▶ FREE DOWNLOAD: Blank Decimal Place Value Chart (PDF File)

Before moving forward, make sure that you have a strong understanding of place value and that you can correctly identify place values, especially for values to the right of a decimal sign.

 

Figure 03: You can use a place value chart to help you to correctly identify the place value of each digit in a number.

 

Keep Learning: Where is the hundredths place value in math?

Since this guide focuses on rounding to the nearest hundredth, here are a few examples of identifying the hundredths and thousandths place value digit for the following numbers.

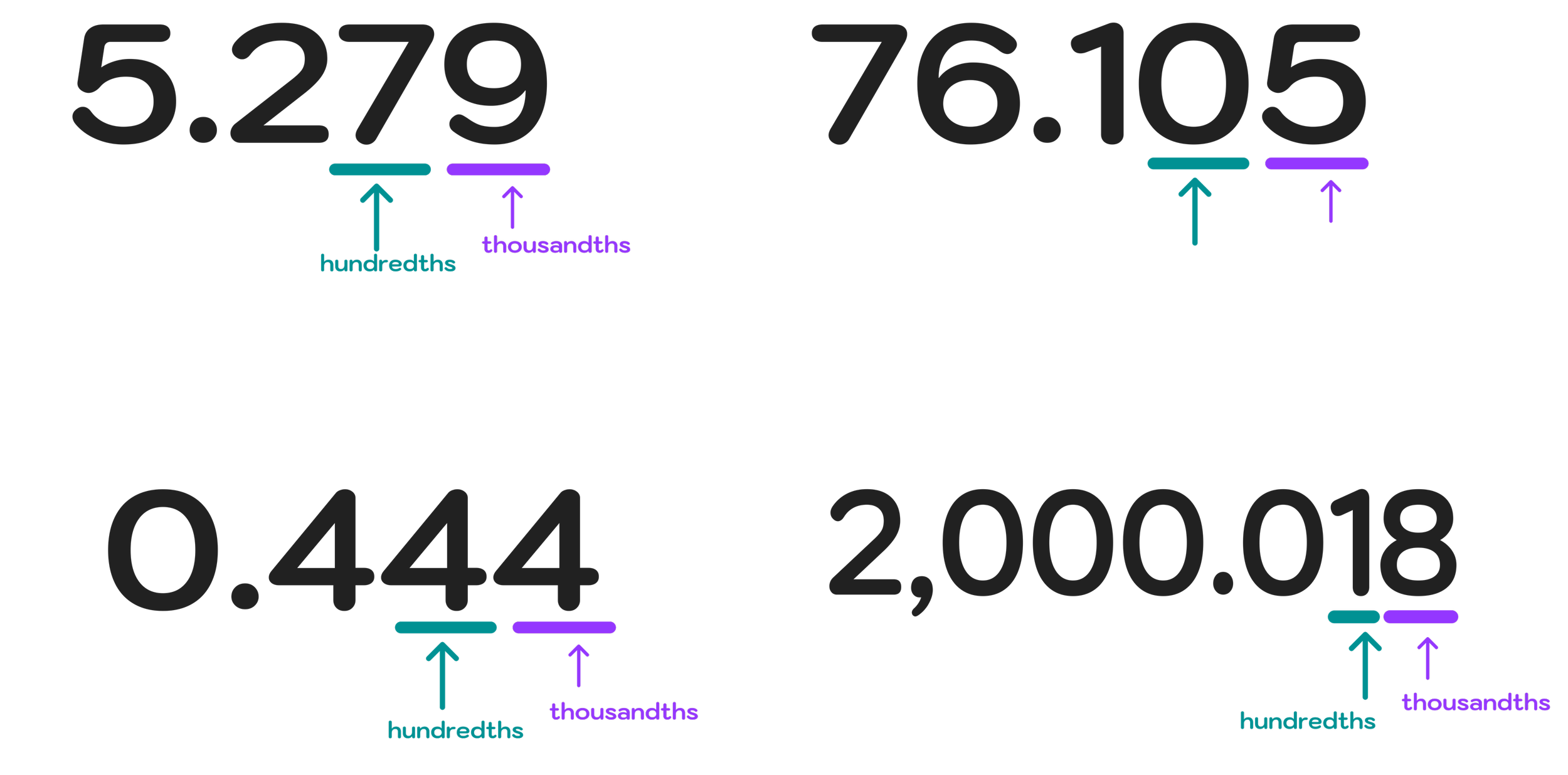
  • 5.279 → 7 is in the hundredths decimal place, 9 is in the thousandths decimal place

  • 76.105 → 0 is in the hundredths decimal place, 5 is in the thousandths decimal place

  • 0.444 → 4 is in the hundredths decimal place, 4 is in the thousandths decimal place

  • 2,000.018 → 1 is in the hundredths decimal place, 8 is in the thousandths decimal place

 

Figure 04: How to identify the hundredths and thousandths decimal places in a given number.

 

How to Round to the Nearest Hundredth using 3 Simple Steps

Ready to work through some practice problems focused on rounding to the nearest hundredth?

For all of the practice problems in this guide, you can use the following 3-step process for rounding to the nearest hundredth:

  • Step One: Identify the value in the thousandths decimal place and ignore all numbers to the right of it

  • Step Two: Determine if the value in the thousandths decimal place is 5 or larger or 4 or smaller

  • Step Three: If the value in the thousandths decimal place is 5 or larger, round the number directly to the left (the value in the hundredths decimal place) up. If the value in the thousandths decimal place is 4 or smaller, round it down to zero.

If these three steps seam confusing at first, that’s okay. They will make more sense once you get some experience applying them to the following practice problems.

Example #1: Round to the Nearest Hundredth: 4.253

Starting off with our first example, we are tasked with rounding the number 4.253 to the nearest hundredth.

We can solve this problem by applying the 3-step method as follows:

Step One: Identify the value in the thousandths decimal place and ignore all numbers to the right of it

For the number 4.253, the 3 is in the thousandths decimal place slot (and there are no additional numbers to the right of it).

 

Figure 05: For the number 4.253, the number 3 is in the thousandths place value slot.

 

Step Two: Determine if the value in the thousandths decimal place is 5 or larger or 4 or smaller

For this example, 3 is in the thousandths place value slot and 3 is 4 or smaller, so we will have to round down in the third and final step.

Step Three: If the value in the thousandths decimal place is 5 or larger, round the number directly to the left (the value in the hundredths decimal place) up. If the value in the thousandths decimal place is 4 or smaller, round it down to zero.

In the last step, we determined that the value in the thousandths place value slot, 3, is 4 or smaller and that we have to round down. When rounding down, we turn that 3 in the thousandths place value slot into a zero, which effectively makes it disappear. Now, we can conclude that:

Final Answer: 4.254 rounded to the nearest hundredth is 4.25

The final answer to Example 1 (and the steps to solving it) is displayed in Figure 06 below.

 

Figure 06: When rounding down, the number in the thousandths decimal spot becomes a zero and disappears.

 

Example #2: Round to the Nearest Hundredth: 4.257

Notice that Example #2 is very similar to Example #1. The only difference is that, in this example, the value of the number in the thousandths place value slot is a 7 (rather than a 3).

Let’s go ahead and apply our 3-step method to see how this difference affects our answer.

Step One: Identify the value in the thousandths decimal place and ignore all numbers to the right of it

For the number 4.257, the 7 is in the hundredths place value slot as illustrated in Figure 07 below.

 

Figure 07: The thousandths place value slot is three digits to the right of the decimal point.

 

Step Two: Determine if the value in the thousandths decimal place is 5 or larger or 4 or smaller

As previously stated, for this example, the value of the number in the thousandths place value slot is a 7, which is 5 or larger.

Step Three: If the value in the thousandths decimal place is 5 or larger, round the number directly to the left (the value in the hundredths decimal place) up. If the value in the thousandths decimal place is 4 or smaller, round it down to zero.

Since the value in the thousandths place value slot is 5 or larger, we have to round up to solve this problem. When rounding up, we have to add one to number in the tenths place value slot (the number directly to the left of the number in the thousandths place value slot) and “zero out” the number in the thousandths place value slot.

Final Answer: 4.257 rounded to the nearest hundredth is 4.26

The entire process of solving this second example is illustrated in Figure 08 below.

 

Figure 08: 4.257 rounded to the nearest thousandth is 4.26.

 

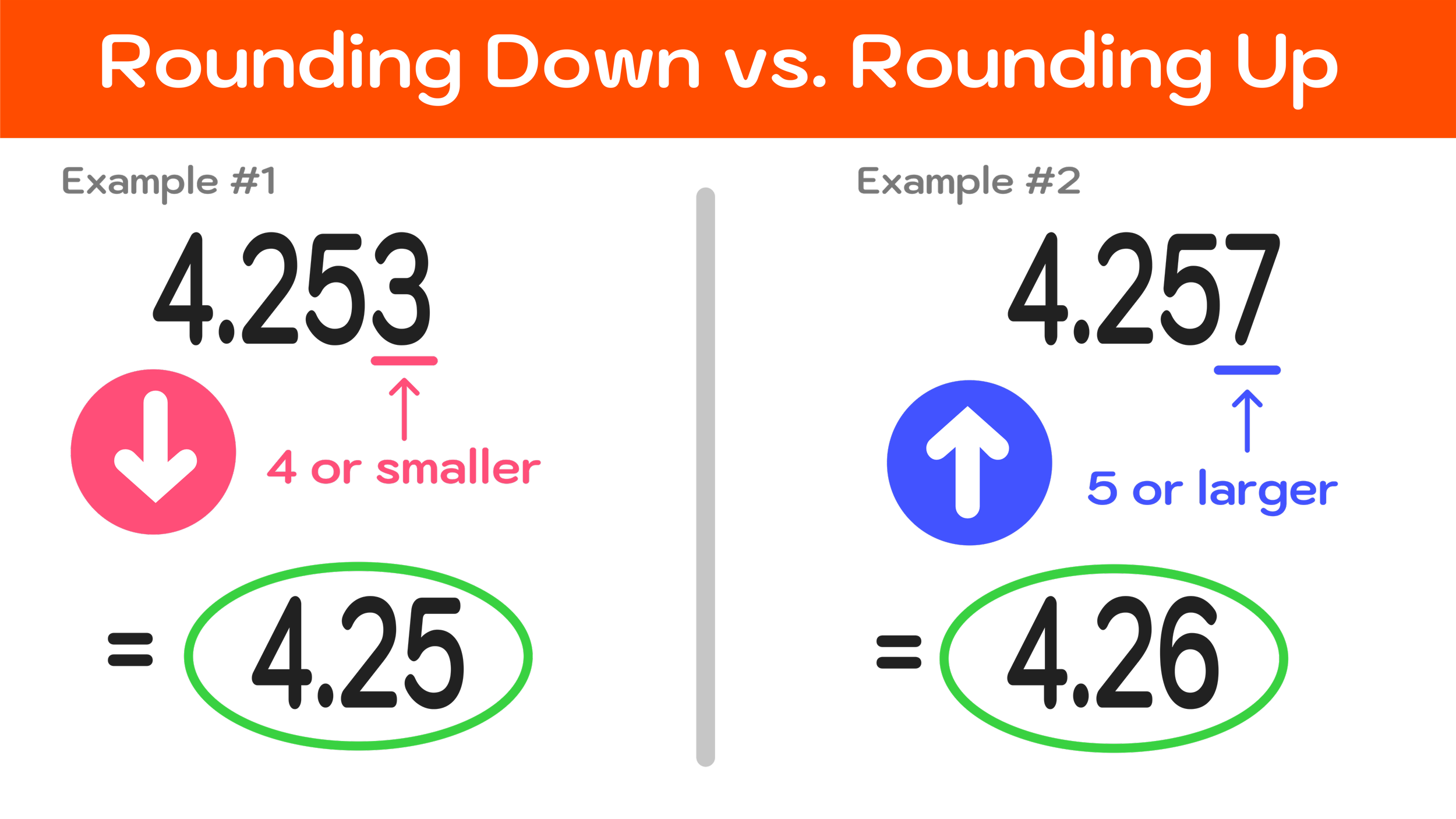
Before we move onto more practice problems, Figure 09 below compares the first two examples. Be sure that you understand the difference between rounding up and rounding down before moving on.

 

Figure 09: Comparing Example #1 (rounding down) and Example #2 (rounding up). What do you notice?

 

Example #3: Round to the Nearest Hundredth: 88.7309

For this third example, notice that there is a digit in the ten-thousandths decimal place (the value four digits to the right of the decimal point). While this number, 88.7309 is larger than the numbers in the first two examples, you can still use the 3-step method for rounding to the nearest hundredth to solve it.

Step One: Identify the value in the thousandths decimal place and ignore all numbers to the right of it

For the number 88.7309, the thousandths place value digit (the number three digits to the right of the decimal point) is 0. Remember that you can ignore any numbers to the right of the digit in the thousandths place value slot (which is the 9 in this example).

For the sake of rounding correctly, you can ignore the 9 and think of this number as 88.730.

 

Figure 10: Remember that you can ignore any numbers to the right of the digit in the thousandths place value slot.

 

Step Two: Determine if the value in the thousandths decimal place is 5 or larger or 4 or smaller

Next, notice that 0 is in the thousandths place value slot. Clearly, 0 is 4 or smaller.

Step Three: If the value in the thousandths decimal place is 5 or larger, round the number directly to the left (the value in the hundredths decimal place) up. If the value in the thousandths decimal place is 4 or smaller, round it down to zero.

Since 0 is 4 or smaller, we will have to round down. Since 0 is already 0, we can just make it disappear and make the following conclusion:

Final Answer: 88.7309 rounded to the nearest hundredth is 88.73

This final answer is shown in Figure 11 below.

 

Figure 11: 88.7309 rounded to the nearest hundredth is 88.73.

 

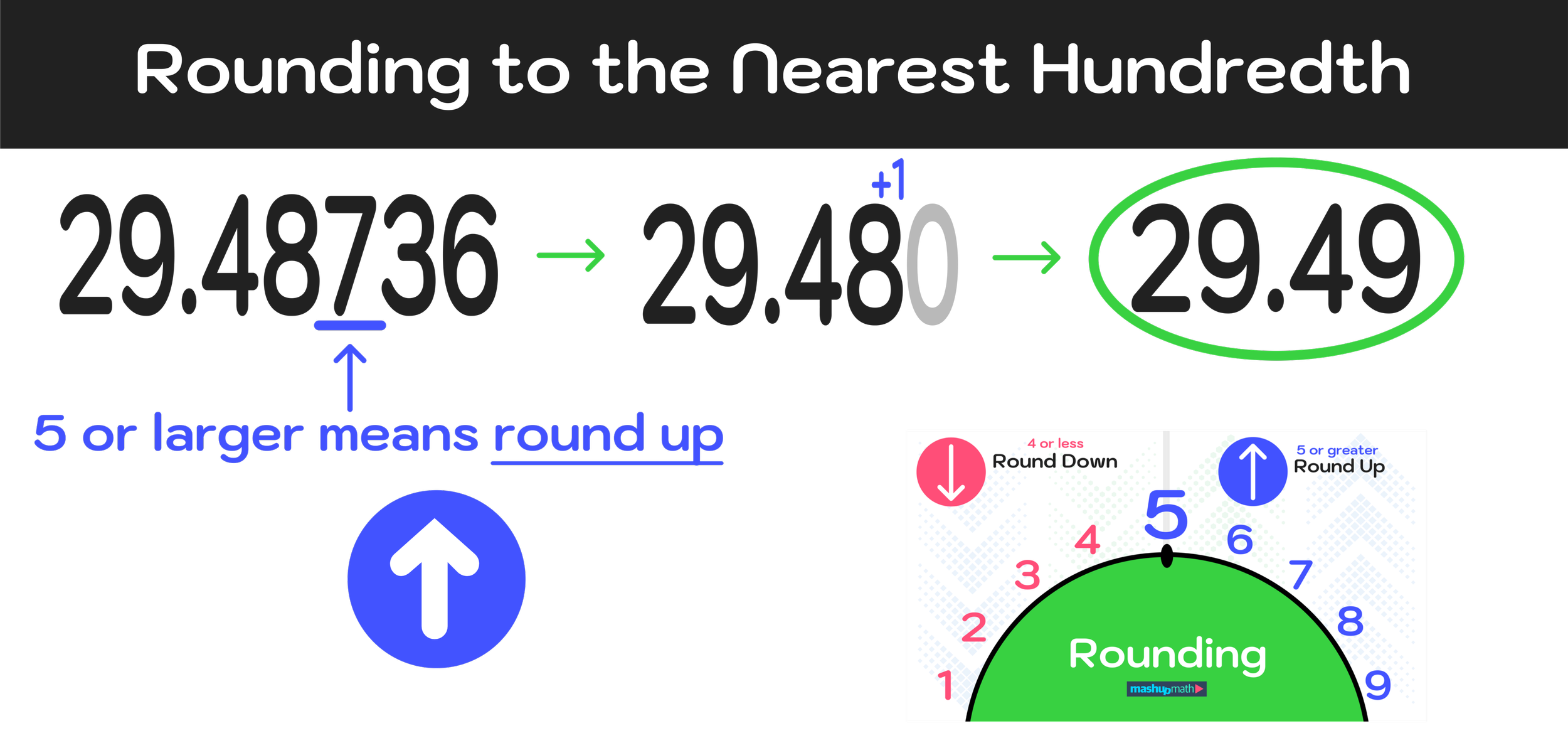
Example #4: Round to the Nearest Hundredth: 29.48736

Similar to the previous example, 29.48736 includes numbers the right of the thousandths decimal place. Remember that you can ignore these numbers and use the three steps to solve this problem as follows:

Step One: Identify the value in the thousandths decimal place and ignore all numbers to the right of it

For the number 29.48736, the number 7 is in the thousandths place value slot.

 

Figure 12: When rounding to the nearest hundredth, the number in the thousandths place value slot will determine if you have to round up or down.

 

Step Two: Determine if the value in the thousandths decimal place is 5 or larger or 4 or smaller

Since 7, the number in the thousandths place value slot, is 5 or larger, we will have to round up in step three.

Step Three: If the value in the thousandths decimal place is 5 or larger, round the number directly to the left (the value in the hundredths decimal place) up. If the value in the thousandths decimal place is 4 or smaller, round it down to zero.

To round this number to the nearest hundredth, you must add one to the 8 in the tenths place value slot and zero out the 7.

Final Answer: 29.48736 rounded to the nearest hundredth is 29.49

The complete three-step process for solving example #5 is shown in Figure 13 below.

 

Figure 13: 90.352 rounded to the nearest tenth is equal to 90.4

 

Example #5: Round to the Nearest Hundredth: 8.495

By now, you should be a bit more comfortable with rounding to the nearest hundredth. Let’s continue on to work through two more examples where we will gain more experience using the 3-step method.

For this next example, we have to round the number 8.495 to the nearest hundredth.

Step One: Identify the value in the thousandths decimal place and ignore all numbers to the right of it

For the number 9.495, the digit in the thousandths place value slot is 5, as shown in Figure 14 below.

 

Figure 14: How to Round to the nearest Hundredth: When the digit in the thousandths place value slot is 5 or larger, you have to round up.

 

Step Two: Determine if the value in the thousandths decimal place is 5 or larger or 4 or smaller

Next, we can see that 5 (digit in the thousandths place value slot) is indeed 5 or larger.

Step Three: If the value in the thousandths decimal place is 5 or larger, round the number directly to the left (the value in the hundredths decimal place) up. If the value in the thousandths decimal place is 4 or smaller, round it down to zero.

Since 5 is 5 or larger, we will have to round up. The number directly to the left of the thousandths digit is a 9, so how do we round it up without turning it into a double-digit number? In the case of rounding up the number 9, you must turn it into a zero and add one to the number directly to its left (this process is illustrated in Figure 15 below).

Final Answer: 8.495 rounded to the nearest hundredth equals 8.50

 

Figure 15: 8.495 rounded to the nearest hundredth equals 8.50

 

Example #6: Round to the Nearest Hundredth: 64.01408

Here is our final practice problem for rounding to the nearest hundredth!

To solve it, let’s go ahead and apply our 3-step method as follows:

Step One: Identify the value in the thousandths decimal place and ignore all numbers to the right of it

For this last problem, the digit in the thousandths place value slot is 4, as shown below in Figure 16. Remember that all of the digits to the right of the 4 can be ignored.

 

Figure 16: Remember that, when it comes to rounding to the nearest tenth, you can ignore any additional numbers that come after the digit in the thousandths decimal slot.

 

Step Two: Determine if the value in the thousandths decimal place is 5 or larger or 4 or smaller

Notice that the value in the thousandths place value slot is a 4, which is 4 or smaller.

Step Three: If the value in the thousandths decimal place is 5 or larger, round the number directly to the left (the value in the hundredths decimal place) up. If the value in the thousandths decimal place is 4 or smaller, round it down to zero.

Since the value in the thousandths place value slot is 4 or smaller, you can round it down to zero. Therefore, the 4 will disappear and we are left with the following result:

Final Answer: 64.01408 rounded to the nearest hundredth is 64.01

 

Figure 17: 64.01408 rounded to the nearest hundredth is 64.01

 

Conclusion: How to Round to the Nearest Hundredth

In math, it is important to know how to estimate and round numbers to make them easier to work with. This skill is especially important when it comes to working with decimal numbers.

By working through this step-by-step tutorial on rounding numbers to the nearest hundredth, you learned a simple 3-step process that you can use to round any number to the nearest hundredth. The 3-steps outlined in this guide are as follows:

Step One: Identify the value in the thousandths decimal place and ignore all numbers to the right of it

Step Two: Determine if the value in the thousandths decimal place is 5 or larger or 4 or smaller

Step Three: If the value in the thousandths decimal place is 5 or larger, round the number directly to the left (the value in the hundredths decimal place) up. If the value in the thousandths decimal place is 4 or smaller, round it down to zero.

Once you understand how to correctly apply these three steps, you can use them to solve any problem that requires you to round to the nearest hundredth. Using this method, we solved six different rounding practice problems where we had to round a given number to the nearest hundredth. Here is a quick review of our results:

  • 4.253 → 4.25

  • 4.257 → 4.26

  • 88.7309 → 88.73

  • 29.48736 → 29.49

  • 8.495 → 8.50

  • 64.01408 → 64.01

Need more help? If so, we suggest going back and working through this step-by-step guide again (practice makes perfect after all). You can also gain some more rounding practice by downloading some free topic-specific worksheets available on our free math worksheet libraries.

Keep Learning:

How to Round to the Nearest Thousandth (Step-by-Step Guide)

Continue your rounding journey by learning how to round to the nearest thousandth.

Comment

How to Round to the Nearest Tenth—Step-by-Step Guide

Comment

How to Round to the Nearest Tenth—Step-by-Step Guide

How to Round to the Nearest Tenth

Step-by-Step Guide: Rounding to the Nearest Tenth in 3 Easy Steps

 

Free Step-by-Step Guide: How to round to the nearest tenth.

 

Learning and understanding how to round numbers is an important and useful math skill that makes working with large numbers faster and easier.

When it comes to rounding decimals, learning how to round the nearest tenth decimal place is a pretty straightforward process provided that you understand a few vocabulary terms, the meaning of place value, and some simple procedure.

This free Step-by-Step Guide on Rounding to the Nearest Tenth will teach you everything you need to know about how to round a decimal to the nearest tenth and it cover the following topics:

Now, lets begin learning how to round to the nearest tenth by recapping some important math vocabulary terms and concepts.

(Looking for help with rounding to the nearest hundredth and rounding to the nearest thousandth?)

What is rounding in math?

In math, rounding is the process of approximating that involves changing a number to a close value that is simpler and easier to work with. Rounding is done by replacing the original number with a new number that serves as a close approximation of the original number.

For example, if a new pair of basketball sneakers costs $99.88, you could use rounding to conclude that you will need $100 to purchase the sneakers. In this example, you would be rounding to the nearest whole dollar and the purpose of rounding would be to replace the actual cost of “ninety-nine dollars and eight-eighty cents” with an approximated value of “one hundred dollars,” since it is simpler and easier to work with.

 

Figure 01: You could use rounding to say that a pair of sneakers that actually costs $99.88 has an approximate cost of $100, since one hundred is simpler and easier to work with.

 

As shown in Figure 01 above, $100 is simpler and easier to work with than $99.88. So, if you had to estimate the cost of 7 pairs of basketball shoes, you could easier estimate that the cost would be $700 (since 7 x 100 = 700).

What is the significance of 5 when it comes to rounding?

The next important thing to remember when it comes to rounding is the significance of the number 5. When you first learn how to perform simple rounding, you may use a visual aid called a rounding hill as shown in Figure 02 below. A rounding hill shows how, when it comes to rounding, if whatever digit you are rounding is less than 5 (4 or less), you will round down. If whatever digit you are rounding is 5 or greater, you will round up. So, 5 is the cutoff for rounding up in any rounding scenario.

  • If digit to the right of the number being rounded is 4 or less → round down

  • If digit to the right of the number being rounded is 5 or greater → round up

For example, if you wanted to round 17 to the nearest ten, the result would be 20 since 7 is 5 or greater and you would have to round up.

  • 17 → 7 is 5 or greater, so round up → 20

Conversely, if you wanted to round 13 to the nearest ten, the result would be 10 since 3 is 4 or less and you would have to round down.

  • 13 → 3 is 4 or less, so round down → 10

 

Figure 02: The Rounding Hill illustrates the significance of 5 and how you can determine when to round up and when to round down.

 

What does rounding to the nearest tenth mean in terms of place value?

Now that you know what rounding is and when to round up or round down, the final concept that we need to review is place value.

In math, place value refers to the numerical value that a digit has by virtue of its position in the number.

For example, consider the number 3.57.

We can think of the number 3.57 as the sum of 3 ones, 5 tenths, and 7 hundredths.

A useful tool for visualizing place value is called a place value chart, where each place value has its own slot so you can clearly identify a given digits place value. Figure 03 below shows the number 3.57 within a place value chart, where you can clearly see that 3 is in the ones place, 5 is in the tenths place, and 7 is in the hundredths place.

▶ FREE DOWNLOAD: Blank Decimal Place Value Chart (PDF File)

 

Figure 03: A place value chart is a useful tool for identify each digit’s place value, especially when you are dealing with decimals.

 

If you want to learn how to round to the nearest tenth, then you will need to be able to correctly identify the place value of the tenths and hundredths place value, otherwise you will struggle to correctly round a decimal to the nearest tenth (more on why this is the case later on in this guide).

Keep Learning: Where is the hundredths place value in math?

Here are a few more examples of correctly identifying the tenths and hundredths decimal places:

  • 4.12 → 1 is in the tenths decimal place and 2 is in the hundredths decimal place

  • 52.783 → 7 is in the tenths decimal place and 8 is in the hundredths decimal place

  • 0.3333 → 3 is in the tenths decimal place and 3 is in the hundredths decimal place

  • 488.60 → 6 is in the tenths decimal place and 0 is in the hundredths decimal place

 

Figure 04: Examples of identifying the tenths and hundredths decimal place for 4.12, 52.783, 0.3333, and 488.6

 

How to Round to the Nearest Tenth in 3 Easy Steps

Now you are ready to work through a few examples where you have to round to the nearest tenth using our easy 3-step method, which works as follows:

  • Step One: Identify the value in tenths place value slot and the hundredths place value slot

  • Step Two: Determine if the value in the hundredths place value slot is 5 or larger or 4 or smaller

  • Step Three: Round the value in the tenths place value slot up or down depending on the result from step two

Let’s continue on to using these three steps to several practice problems.

Example #1: Round to the Nearest Tenth: 8.63

This first example is pretty simple. You are tasked with rounding to the nearest tenth the number 8.63.

Let’s go ahead and apply our 3-step method to solving this problem:

Step One: Identify the value in tenths place value slot and the hundredths place value slot

In this case, 6 is in the tenths place value slot and 3 is in the hundredths place value slot as shown in Figure 05 below.

 

Figure 05: For the number 8.63, 6 is in the tenths place value slot and 3 is in the hundredths place value slot.

 

Step Two: Determine if the value in the hundredths place value slot is 5 or larger or 4 or smaller

For this example, 3 is in the hundredths place value slot. Since 3 is less than 5, we will have to round down in the final step.

Step Three: Round the value in the tenths place value slot up or down depending on the result from step two

As determined in step two, we will be rounding the hundredths place value digit, which is 3 in this example, down to zero. This effectively means that, when rounding to the nearest tenth, you must remove the hundredths value digit entirely and make the following conclusion:

Final Answer: 8.63 rounded to the nearest tenth is 8.6

This final result is illustrated in Figure 06 below. Now, let’s move onto a second example where you will have to round up to get your final answer.

 

Figure 06: Step One: Split the cubic polynomial into two groups

 

Example #2: Round to the Nearest Tenth: 32.87

For this next example, you can use the same 3-step approach to determine what is 32.8 rounded to the nearest tenth as follows:

Step One: Identify the value in tenths place value slot and the hundredths place value slot

For the number 32.87, 8 is in the tenths place value slot and 7 is in the hundredths place value slot as shown in Figure 07.

 

Figure 07: Rounding to the nearest tenth: The first step is to identify the digits in the tenths and hundredths place value slots.

 

Step Two: Determine if the value in the hundredths place value slot is 5 or larger or 4 or smaller

For the second example, 7 is in the hundredths place value slot. Since the number 7 is greater than 5, we will have to round up in the last step.

Step Three: Round the value in the tenths place value slot up or down depending on the result from step two

We have already determined that finding 32.87 rounded to the nearest tenth will require rounding up. In this case, the 8 in the tenths decimal place will round up to a 9 and the hundredths decimal place will disappear.

Final Answer: 32.87 rounded to the nearest tenth is 32.9

This final answer is shown in Figure 08 below.

 

Figure 08: 32.87 rounded to the nearest tenth is 32.9

 

Example #3: Round to the Nearest Tenth: 119.308

Notice that this example includes a digit in the thousandths decimal place. While this is a larger number than the previous two examples, you can still use the 3-step process to find the value of 119.308 rounded to the nearest tenth.

Step One: Identify the value in tenths place value slot and the hundredths place value slot

In this example, for the number 119.308, 3 is in the tenths decimal place value slot, 0 is in the hundredths place value slot, and 8 is in the thousandths place value slot (although the 8 will not have any effect on how you solve this problem, and you can actually ignore it entirely and still correctly round 119.308 to the nearest tenth).

 

Figure 09: To find the value of 119.308 rounded to the nearest tenth, you only need to worry about the values in the tenths and hundredths place value slots (anything after that does not matter).

 

Step Two: Determine if the value in the hundredths place value slot is 5 or larger or 4 or smaller

Continuing on, lets focus on the fact that 0 is in the hundredths place value slot for this third example.

Step Three: Round the value in the tenths place value slot up or down depending on the result from step two

Since 0 is less than 5, we will have to round it down to—zero. And since zero is already zero, all that you have to do is make it disappear entirely and conclude that:

Final Answer: 119.308 rounded to the nearest tenth is 119.3

This final answer is shown in Figure 10 below.

 

Figure 10: How to round to the nearest tenth: 119.308 can be rounded to 119.3

 

Example #4: Round to the Nearest Tenth: 90.352

Just like the last example, 90.352 includes a digit in the thousandths decimal place. And, just like the last example, you can ignore that digit entirely and apply the same 3-step method as follows:

Step One: Identify the value in tenths place value slot and the hundredths place value slot

The place value slots for 90.352 are as follows: 3 is in the tenths place value slot and 5 is in the hundredths place value slot. Again, you can ignore the 2 in the thousandths place value slot.

 

Figure 11: How to round to the nearest tenth: start by identifying the values of the tenths and hundredths place value digits

 

Step Two: Determine if the value in the hundredths place value slot is 5 or larger or 4 or smaller

For the second step, our focus is on the 5 in the hundredths place value slot.

Step Three: Round the value in the tenths place value slot up or down depending on the result from step two

Since 5 is equal to 5 or greater, we will have to round up. Remember that 5 is the cutoff for rounding up, so this is an example where the number just meets the requirements for rounding up instead of down.

Final Answer: 90.352 rounded to the nearest tenth is 90.4

The entire process for solving example #4 is illustrated in Figure 12 below.

 

Figure 12: 90.352 rounded to the nearest tenth is equal to 90.4

 

Example #5: Round to the Nearest Tenth: 149.96

Are you starting to get the hang of using the three-step process to round numbers to the nearest tenth? Let’s try rounding 149.96 to the nearest tenth and find out:

Step One: Identify the value in tenths place value slot and the hundredths place value slot

For this fifth example, the digit in the tenths place value slot is 9 and the digit in the hundredths place value slot is 6, as shown in Figure 13 below.

 

Figure 13: The digit in the tenths place value slot is 9 and the digit in the hundredths place value slot is 6.

 

Step Two: Determine if the value in the hundredths place value slot is 5 or larger or 4 or smaller

Moving on, note that the digit in the hundredths place value slot is 6, which is 5 or larger.

Step Three: Round the value in the tenths place value slot up or down depending on the result from step two

Since 6 is equal to 5 or greater, we will have to round up. However, notice that the digit in the tenths place value slot is a 9, which can not be rounded up to the next digit. In this case, the 9 will become a zero and the digit that gets rounded up is the one in the ones place value slot (the number directly to the left of the decimal point).

So, when you round 149.96 to the nearest tenth, the 9 becomes a zero and the number 149 gets rounded up to the next whole number as follows:

Final Answer: 149.96 rounded to the nearest tenth equals 150.0

 

Figure 14: 149.96 rounded to the nearest tenth is 150.0

 

Example #6: Round to the Nearest Tenth: 3.0499

Now let’s work through one final example of rounding a number to the nearest tenth.

Remember that you only need to know the digits in the tenths and hundredths place value slots to round correctly, and you can ignore any additional numbers.

Step One: Identify the value in tenths place value slot and the hundredths place value slot

For this final example, the digit in the tenths place value slot is 0 and the digit in the hundredths place value slot is 4, as illustrated in Figure 15 below.

 

Figure 15: Remember that, when it comes to rounding to the nearest tenth, you can ignore any additional numbers that come after the digit in the thousandths decimal slot.

 

Step Two: Determine if the value in the hundredths place value slot is 5 or larger or 4 or smaller

Just as we did in all of the previous examples, the second step requires you to identify the value of the hundredths place value digit. For the number 3.0499, this value is 4.

Step Three: Round the value in the tenths place value slot up or down depending on the result from step two

4, the digit in the hundredths place value slot, is less than 5, so we will be rounding down. So, the disappears and the 0 in the tenths place value slot stays a 0 since it can not be rounded down any further.

Therefore, we can conclude that:

Final Answer: 3.0499 rounded to the nearest tenth equals 3.0

 

Figure 16: 3.0499 rounded to the nearest tenth is 3.0

 

How to Round to the Nearest Tenth: Conclusion

Rounding is an important math skill that every student must learn at some point. While rounding integers is relatively simple, the process, while similar, gets trickier when decimals are involved.

This step-by-step guide focused on teaching you how to round numbers to the nearest tenth (i.e. to the nearest tenth decimal place). By using the following 3-step method, you can successfully round any number involving decimals to the nearest tenth:

Step One: Identify the value in tenths place value slot and the hundredths place value slot

Step Two: Determine if the value in the hundredths place value slot is 5 or larger or 4 or smaller

Step Three: Round the value in the tenths place value slot up or down depending on the result from step two

This method will work for rounding any number to the nearest tenth. To recap, we used this method to solve the following examples where we were given a decimal number and tasked with rounding it to the nearest tenth:

  • 8.63 → 8.6

  • 32.87 → 32.9

  • 119.309 → 119.3

  • 90.352 → 90.4

  • 149.96 → 150.0

  • 3.0499 → 3.0

If you need more practice, we recommend working through the six practice problems in this guide again and/or working through the free rounding practice worksheets available on our free math worksheet libraries.

Keep Learning:

How to Round to the Nearest Hundredth (Step-by-Step Guide)

Continue your rounding journey by learning how to round to the nearest hundredth.

Comment

How to Divide Decimals Explained—Step-by-Step Examples and Tutorial

1 Comment

How to Divide Decimals Explained—Step-by-Step Examples and Tutorial

How to Divide Decimals Explained in 3 Easy Steps

Step-by-Step Guide: How to Divide Decimals by Whole Numbers and How to Solve Decimal Divided by Decimal Problems

 

Free Step-by-Step Guide: Dividing Decimals Explained in 3 Easy Steps

 

In math, it is important to be able to work with and perform operations on decimals, which are numbers in the base-10 system that include a point that separates the whole number(s) from the attached fractional parts. For example, the number 2.5 is a decimal number that represents two and a half.

One of the more challenging operations to perform with decimals is division. However, if you know how to divide whole numbers, then you can easily learn how to divide decimals using just a few simple steps. Note that there are two different cases when it comes to dividing decimals: a decimal divided by a whole number and a decimal divided by another decimal. We will cover both cases in this guide.

Below are quick links to each section of this free Step-by-Step Guide on How to Divide Decimals:

While learning how to divide with decimals can be intimidating at first, it is a math skill that you can easily learn with practice following a simple 3-step process. This free dividing with decimals tutorial will teach you everything you need to know about how to divide with decimals, including several step-by-step practice problems for both dividing decimals by whole numbers and dividing decimals by decimals.

But, before we dive into our practice problems, let’s do a quick recap of some important vocabulary terms related to division as well as a quick review of how to perform long division. If you are already comfortable with the review information, you can use the quick links above to skip ahead to the section that best meets your needs.

 

Figure 01: How to Divide Decimals: Key Vocabulary

 

What is a dividend? What is a divisor?

In this guide on dividing decimals, we will be using the terms dividend and divisor often, so make sure that you are familiar with what they mean:

  • When dividing two numbers, the dividend is the number that is being divided.

  • When dividing two numbers, the divisor is the number of parts the dividend is being divided into.

For example, consider the division problem: 248 ÷ 8

  • 248 is the dividend because it is the number being divided

  • 8 is the divisor because 248 is being divided into 8 parts.

This example is illustrated in Figure 01 above.

Because this guide will be teaching you how to divide decimals without using a calculator, we will be using long division to solve problems. Therefore, it is important that you are familiar with the divisor/dividend notation shown in Figure 01 above, where: 248 ÷ 8 → 8 | 248

Now that you know how to identify a dividend and a divisor and the divisor/dividend notation, lets do a quick review of how to perform long division using the same example of 248 ÷ 8.

 

Figure 02: Dividing Decimals Explained: Long Division Review

 

Figure 02 above shows a step-by-step review of how to use long division to determine that 248 ÷ 8 = 31.

If you are not comfortable with performing long division, then we recommend that you pause now and do a deeper review before moving forward with this tutorial on how to divide decimals.

How to Divide Decimals by Whole Numbers

The first set of examples in this dividing decimals tutorial will focus on how to divide decimals by whole numbers and will include examples for when the dividend is the whole number and when the divisor is the whole number as well.

How to Divide Decimals by Whole Numbers

Example #1: 1.5 ÷ 2

Let’s start off with a simple example that you could probably solve without the use of long division (although we will solve it using long division anyway so that you can start to become more familiar with our 3-step process for dividing decimals).

For this example, and all of the examples that follow, you will be using the following three step method for dividing decimals:

  • Step One: Identify the dividend and the divisor and determine whether or not the divisor is a whole number (if it is, move onto Step Three).

  • Step Two: If the divisor is not a whole number, multiply it by a multiple of 10 to make it a whole number (multiply tenths by 10, hundredths by 100, thousandths by 1,000, etc.). Whatever multiple of 10 that you multiplied the divisor by, you must also multiply the dividend by.

  • Step Three: Use long division to solve.

We will be applying this 3-step process of all of the dividing decimals practice problems in this guide, so don’t get intimidated if you are a little confused right now. The process will make more sense and be easier to apply after we work through a few examples.

 

Figure 03: How to Divide Decimals: First, identify whether or not the divisor is a whole number.

 

Lets start with the first step:

Step One: Identify the dividend and the divisor and determine whether or not the divisor is a whole number (if it is, move onto Step Three).

In the case of 1.5 ÷ 2

  • 2 is the divisor

  • 1.5 is the dividend

As shown in Figure 03 above, it is clear that the divisor is 2, which is indeed a whole number, so, for this example, we can skip the second step and move right onto Step Three.

Also notice that in Figure 03 above, we rewrote 1.5 as 1.50 (they both mean the same thing). Adding extra zeros after the last digit of a decimal does not change the number and often helps you to perform long division, as you will see in the next step.

Step Three: Use long division to solve.

All that you have to do now is use long division to solve the problem. You can click play on the video below to see an animated step-by-step breakdown of how to perform the long division for this problem.

Based on the video and the illustrated summary shown in Figure 04 below, you can see that:

Solution: 1.50 ÷ 2 = 0.75

This solution should make sense because dividing 1.50 in half will result in 0.75. Before moving onto another similar example of a decimal divided by a whole number, we encourage you to review the above review as we will not include videos for every example.

 

Figure 04: How to Divide Decimals by Whole Numbers: Example #1 Solved

 

Dividing Decimals by Whole Numbers

Example #2: 24.36 ÷ 3

For this next example, we will be using the exact same three-step approach as Example #1.

Step One: Identify the dividend and the divisor and determine whether or not the divisor is a whole number (if it is, move onto Step Three).

For this example:

  • 3 is the divisor

  • 24.36 is the dividend

Since the divisor in this example is a whole number (3), we can skip the second step just like we did in the previous example and move onto the third and final step.

Step Three: Use long division to solve.

To solve the second example, perform long division just as you did to solve Example #1. Remember to follow your steps carefully and to line up your decimal points.

The entire process of using long division to solve 24.36 ÷ 3 is illustrated in Figure 05 below.

 

Figure 05: Dividing decimals by whole numbers explained.

 

After completing Step Three, we can conclude that:

Solution: 24.36 ÷ 3 = 8.12

Now, lets look at a few examples of a decimal divided by a whole number where the divisor is not a whole number.

How to Divide Decimals by Whole Numbers

Example #3: 92 ÷ 2.3

For this third example of dividing decimals by whole numbers, we will again be using the same three-step method as the previous two examples (as well as all on the examples that will follow this one), except that this time we will not be able to skip the second step.

Step One: Identify the dividend and the divisor and determine whether or not the divisor is a whole number (if it is, move onto Step Three).

In this case:

  • 2.3 is the divisor

  • 92 is the dividend

Since the divisor in this example is 2.3, which is not a whole number, we will have to move onto the second step (which we were able to skip in the previous two examples).

Step Two: If the divisor is not a whole number, multiply it by a multiple of 10 to make it a whole number (multiply tenths by 10, hundredths by 100, thousandths by 1,000, etc.). Whatever multiple of 10 that you multiplied the divisor by, you must also multiply the dividend by.

When it comes to dividing decimals, we cannot have a decimal as a divisor. However, we can multiply both the divisor and the dividend by the same multiple of ten to transform the divisor into a whole number and still have a proportional relationship.

Since the final digit of 2.3 is in the tenths place value slot, we will multiply both the divisor (2.3) and the dividend (92) by 10 as shown below and in Figure 06:

  • 2.3 x 10 = 23

  • 92 x 10 = 920

*Remember that what you do to one number, you must do to the other number. If you forget to multiply both the dividend and the divisor by 10, you will get the wrong answer.

 

Figure 06: How to Divide Decimals by Whole Numbers: The divisor has to be a whole number.

 

Step Three: Use long division to solve.

After completing Step Two, all we have to do is use long division to solve 920 ÷ 23.

The step-by-step process for using long division to divide 920 by 23 is shown in Figure 07 below.

 

Figure 07: Decimal divided by a whole number

 

Finally, we can say that:

Solution: 92 ÷ 2.3 = 40

Next, lets look at one final example of how to divide decimals by whole numbers before we move onto learn all about dividing decimals by decimals.

How to Divide Decimals by Whole Numbers

Example #4: 16 ÷ 6.25

Step One: Identify the dividend and the divisor and determine whether or not the divisor is a whole number (if it is, move onto Step Three).

For the fourth example, the divisor is a decimal and the dividend is a whole number.

  • 6.25 is the divisor

  • 16 is the dividend

Step Two: If the divisor is not a whole number, multiply it by a multiple of 10 to make it a whole number (multiply tenths by 10, hundredths by 100, thousandths by 1,000, etc.). Whatever multiple of 10 that you multiplied the divisor by, you must also multiply the dividend by.

Since the divisor is a decimal (6.25), we will have to multiply both the divisor and the dividend by the same multiple of ten.

And since, in this example, the final digit of the divisor, 6.25, is in the hundredths place value slot, we will multiply both the divisor and the dividend by 100 as shown below and in Figure 08.

  • 6.25 x 100 = 625

  • 16 x 100 = 1,600

 

Figure 08: How do you divide decimals by whole numbers?

 

After completing long division, we can conclude that:

Solution: 16 ÷ 6.25 = 2.56

Now we will move on from dividing decimals by whole numbers to learning how to divide decimals by decimals.

Dividing Decimals by Decimals

This section of our guide focused on dividing decimals by decimals. If you used the quick links at the top of the page to skip to this section, we recommend working through the examples in the dividing decimals by whole numbers section above, because it will help you to better understand how to use the following three-step method for dividing decimals by decimals:

  • Step One: Identify the dividend and the divisor and determine whether or not the divisor is a whole number (if it is, move onto Step Three).

  • Step Two: If the divisor is not a whole number, multiply it by a multiple of 10 to make it a whole number (multiply tenths by 10, hundredths by 100, thousandths by 1,000, etc.). Whatever multiple of 10 that you multiplied the divisor by, you must also multiply the dividend by.

  • Step Three: Use long division to solve.

Just as the previous section on dividing decimals by whole numbers, we will be following the same steps for dividing decimals by decimals.

Lets go ahead and dive into the first example.

How to Divide with Decimals

Example #1: 7.68 ÷ 0.4

Step One: Identify the dividend and the divisor and determine whether or not the divisor is a whole number (if it is, move onto Step Three).

For this first example:

  • 0.4 is the divisor

  • 7.68 is the dividend

For all of the examples in this section, we will be dividing decimals by decimals, so it will always be the case that the divisor is not a whole number. Therefore, you will always have to move onto Step Two, where you will use multiplication to transform the divisor into a whole number.

Step Two: If the divisor is not a whole number, multiply it by a multiple of 10 to make it a whole number (multiply tenths by 10, hundredths by 100, thousandths by 1,000, etc.). Whatever multiple of 10 that you multiplied the divisor by, you must also multiply the dividend by.

Again, a decimal divided by a decimal can not be solve using long division when the divisor is not a whole number. Luckily, you can easily transform the divisor into a whole number by multiplying both the divisor and the dividend by a multiple of ten and still have a proportional relationship where you can use long division to solve the problem.

Since the final digit of 0.4 is in the tenths place value slot, you can multiply both the divisor (0.4) and the dividend (7.68) by 10 as shown below and as illustrated in Figure 09.

  • 0.4 x 10 = 4

  • 7.68 x 10 = 76.8

*Always remember that whenever you multiply the divisor by a multiple of 10, you also have to multiply the dividend by that same multiple of 10. If you forget to multiply both by the same multiple of 10, you will not be able to correctly solve the problem.

 

Figure 09: How to Divide with Decimals: Use multiples of 10 to transform the divisor into a whole number.

 

Step Three: Use long division to solve.

Now that you have transformed the divisor into a whole number, you can use long division to solve the problem. You can click play on the video below to see an animated step-by-step breakdown of how to perform the long division for this problem.

Based on the video and the illustrated summary shown in Figure 10 below, we can conclude that:

Solution: 7.68 ÷ 0.4 = 19.2

Before you continue onto the next example of how to divide decimals by decimals, we highly recommend that you review the step-by-step long division tutorial above as we will not include video tutorials for every problem.

 

Figure 10: How to divide decimals by decimals.

 

How to Divide Decimals by Decimals

Example #2: 38.4 ÷ 0.24

Just like the previous example, we will use our three step method to solve a decimal divided by a decimal problem.

Step One: Identify the dividend and the divisor and determine whether or not the divisor is a whole number (if it is, move onto Step Three).

For this first example:

  • 0.24 is the divisor

  • 38.4 is the dividend

Step Two: If the divisor is not a whole number, multiply it by a multiple of 10 to make it a whole number (multiply tenths by 10, hundredths by 100, thousandths by 1,000, etc.). Whatever multiple of 10 that you multiplied the divisor by, you must also multiply the dividend by.

Since the divisor, 0.24, is a decimal, you will have to multiply it (and the dividend) by a power of ten to make it a whole number. Since the last digit of 0.24 is in the hundredths place value slot, we will multiply both the divisor and the dividend by 100 as shown below and in Figure 11.

  • 0.24 x 100 = 24

  • 38.4 x 100 = 3,840

 

Figure 11: Solving a decimal divided by a decimal problems.

 

Step Three: Use long division to solve.

Finally, you now have a divisor that is a whole number, so you can simply use long division to solve 3,840 ÷ 24 to find the solution to this problem, as illustrated in Figure 12 below.

 

Figure 12: How to Divide Decimals Step-by-Step

 

Solution: 38.4 ÷ 0.24 = 160

Now, lets work through one final example.

How to Divide Decimals by Decimals

Example #3: 4.76 ÷ 1.36

Step One: Identify the dividend and the divisor and determine whether or not the divisor is a whole number (if it is, move onto Step Three).

For this first example:

  • 1.36 is the divisor

  • 4.76 is the dividend

Step Two: If the divisor is not a whole number, multiply it by a multiple of 10 to make it a whole number (multiply tenths by 10, hundredths by 100, thousandths by 1,000, etc.). Whatever multiple of 10 that you multiplied the divisor by, you must also multiply the dividend by.

Since the divisor, 1.36, is a decimal, you will have to multiply it (and the dividend) by 100 to transform it into a whole number (we chose to multiply the dividend and the divisor by 100 because the last digit of 1.36 is in the hundredths decimal slot).

  • 1.36 x 100 = 136

  • 4.76 x 100 = 476

Step Three: Use long division to solve.

Now you can find the solution by using long division to solve 476 ÷ 136 as shown in Figure 13 below.

 

Figure 13: Dividing decimals example #3 solution.

 

Solution: 4.76 ÷ 1.36 = 3.5

Dividing Decimals Worksheet

Are you looking for some extra practice with solving problems involving dividing decimals?

You can click the link below to download your free Dividing Decimals Worksheet, which includes a complete answer key so you can check your work. Be sure to apply the three-step process shared in this guide (and also featured on the worksheet) when solving the problems.

▶ Download Your Free Dividing Decimals Worksheet (w/ Answer Key)

▶ Access More Free Topic-Specific Math Worksheets

Dividing Decimals Worksheet Preview

Conclusion: How to Divide Decimals

Learning how to divide decimals by whole numbers or other decimals is an important math skill that every student will eventually have to learn how to do.

While dividing decimals can seem challenging, as long as you know how to perform long division, you can easily solve dividing decimals problems by using the following 3-step approach:

  • Step One: Identify the dividend and the divisor and determine whether or not the divisor is a whole number (if it is, move onto Step Three).

  • Step Two: If the divisor is not a whole number, multiply it by a multiple of 10 to make it a whole number (multiply tenths by 10, hundredths by 100, thousandths by 1,000, etc.). Whatever multiple of 10 that you multiplied the divisor by, you must also multiply the dividend by.

  • Step Three: Use long division to solve.

By working through the examples in this guide as well as the practice problems on the free dividing decimals worksheet, you will gain invaluable practice and experience with dividing decimals, which will make solving problems where you have to divide decimals a simple and easy task.

Keep Learning:

1 Comment

How to Factorize a Cubic Polynomial

1 Comment

How to Factorize a Cubic Polynomial

How to Factorize a Cubic Polynomial

Step-by-Step Guide: How to Factor a Cubic Polynomial in 3 Easy Steps

 

Free Step-by-Step Guide: How to factor a polynomial with a specific number of terms

 

In algebra, a cubic polynomial is an expression made up of four terms that is of the form:

  • ax³ + bx² + cx + d

Where a, b, c, and d are constants, and x is a variable. Polynomials in this form are called cubic because the highest power of x in the function is 3 (or x cubed).

Unlike factoring trinomials, learning how to factorize a cubic polynomial can be particularly tricky because using any type of guess-and-check method is extremely difficult. However, you can easily learn how to factor a cubic polynomial by using the grouping method described in this guide.

This free Step-by-Step Guide on How to Factorize a Cubic Polynomial will cover the following key topics:

While learning how to factor cubic polynomials can be challenging at first, you can develop your skills pretty quickly just by working through practice problems step-by-step until you become more comfortable with factoring cubic polynomials. So, this guide was designed to teach you everything you need to know about how to factor a cubic polynomial. We recommend that you read through this guide from start to finish and work through each example by following along step-by-step. By the end, you will be able to quickly and accurately factorize a cubic polynomial.

 

Figure 01: How to Factorize a Cubic Polynomial

 

What is a cubic polynomial?

As previously mentioned, a cubic polynomial is a math expression that is of the form ax³ + bx² + cx + d, where a, b, c, and d are all constants and x is a variable, and typically has four terms. Note that x is not the only letter that can be used as a variable in a cubic polynomial. Also, the number in front of any variable is referred to as a coefficient.

Additionally, the terms of a cubic polynomial are the individual “pieces” of the expression, separated by an addition or subtraction sign.

For example, the cubic polynomial in Figure 01 above, x³ + 3x² + 2x + 6 has four terms:

  • 1st Term: x³

  • 2nd Term: 3x²

  • 3rd Term: 2x

  • 4th term: 6

Before you can learn how to factor a cubic polynomial, it is extremely important that you know how to recognize that given polynomial is cubic, so make sure that you deeply understand what a cubic polynomial is before moving forward in this guide.

 

Figure 02: Factoring a Cubic Polynomial

 

What does it mean to factorize a cubic polynomial?

In math, the factors of any polynomial represent components or “building blocks” of the polynomial. Whenever you factor a polynomial (cubic or otherwise), you are finding simpler polynomials whose product equals the original polynomial. Each of these simpler polynomials is considered a factor of the original polynomial.

For example, the binomial x² - 100 has two factors (x + 10) and (x-10).

Why? Lets take a look at what happens when we find the product of the factors by double distributing:

  • (x+10)(x-10) = x² + 10x - 10x - 100 = x² + 0 - 100 = x² - 100

Notice that the result was the original polynomial, x² - 100.

Since cubic polynomials (four terms) are more complex than binomials (two terms), their factors will also be a little more complex, but the idea is still the same—factoring a cubic polynomial involves finding simpler polynomials or “building blocks” whose product is the original cubic polynomial.

And, to factorize a cubic polynomial, we will be using a strategy called grouping that will allow you to factor any cubic polynomial (assuming that it is factorable at all) using 3 easy steps. So, lets go ahead and work three practice problems to give you some experience with factoring cubic polynomials by grouping.

Now that you understand the key terms and the difference between a polynomial with 2 terms, 3 terms, and 4 terms.

For factoring each type of polynomial, we will look at two methods: GCF, direct factoring, and, sometimes, a combination of the two.

Let’s get started!

How to a Factorize a Cubic Polynomial Examples

Now, you will learn how to use the follow three steps to factor a cubic polynomial by grouping:

Step One: Split the cubic polynomial into two groups of binomials.

Step Two: Factor each binomial by pulling out a GCF

Step Three: Identify the factors

As long as you follow these three steps, you can easily factor a given polynomial, though note that not all cubic polynomials are factorable."

We will start by factoring the cubic polynomial shown in Figure 01: x³ + 3x² + 2x + 6

Example #1: Factor x³ + 3x² + 2x + 6

 

Figure 03: We have to find the factors of x³ + 3x² + 2x + 6

 

To factorize this cubic polynomial, we will be applying the previously mentioned 3-step method as follows:

Step One: Split the cubic polynomial into groups of two binomials.

To factor this cubic polynomial, we will be using the grouping method, where the first step is to split the cubic polynomial in half into two groups.

 

Figure 04: The first step to factoring a cubic polynomial is to split it into groups of two binomials.

 

For Example #1, at the end of the first step, you have split the cubic binomial down the middle to form two groups of binomials:

  • (x³ + 3x²)

  • (2x + 6)

Why are you splitting the cubic polynomial like this? Notice that it is not possible to pull a Greatest Common Factor (GCF) out of the original cubic polynomial x³ + 3x² + 2x + 6. The goal of the first step is to create two separate binomials, each with a GCF that can be “pulled out.”

 

Figure 05: Make sure that each individual binomial has a GCF before moving onto the next step.

 

Step Two: Factor each binomial by pulling out a GCF

Again, the purpose of the first step is to split the cubic polynomial into two binomials, each with a GCF. Before moving forward, ensure that each individual binomial has a GCF; otherwise, you may need to swap the positions of the middle terms (3x² and 2x). Swapping these middle terms is not required for this first example; however, we will work through an example later on where this is required.

Now, for step two, you can divide the GCF out of each grouping as follows:

  • (x³ + 3x²)→ x²(x +3)

  • (2x + 6) → 2(x + 3)

This process of pulling the GCF out of each binomial is illustrated in Figure 05 below.

 

Figure 06: To factorize a cubic function, split it into two groups and then pull a GCF out of each group.

 

Step Three: Identify the factors

After completing the second step, you are left with:

  • x²(x +3) + 2(x+3)

Notice that both groups share a common term, which, in this case, is (x+3). This result is expected and is a signal that you are factoring the cubic polynomial correctly. If the groups do not share a common terms, then it is likely that the cubic polynomial is not factorable or that you made a mistake pulling out the GCF.

However, since you factored each group and ended up with a common factor of (x+3), you can move on to determining the factors of the cubic polynomial.

The illustration in Figure 06 above color-codes how you use the results from step two to determine the factors of the cubic polynomial.

You already know that one of the factors is (x+3). To find the other factor, you can simply take the two “outside” terms, in this case, x² and +2.

  • x²(x +3) + 2(x+3) → (x²+2)(x+3)

Final Answer: The factors of x³ + 3x² + 2x + 6 are (x²+2) and (x+3)

The entire 3-step method that we just used to factor a cubic polynomial by grouping is shown in Figure 07 below:

 

Figure 07: How to factorize a cubic polynomials step-by-step

 

How can you check if your factors are actually correct? You can perform double distribution to multiply the binomials together to see if the result is indeed the cubic polynomial that you started with. If it is, then you know that you have factorized correctly.

You can see in Figure 08 below that multiplying the factors together does indeed result in the original cubic polynomial, so you know that your factors are correct:

  • (x²+2)(x+3) = x³ + 3x² + 2x + 6

 

Figure 08: Check your answer using double distribution

 

Now, lets go ahead and work through another example of how to factor a cubic polynomial.

Example #2: Factor 2x³ - 3x² + 18x - 27

Just like in the first example problem, you can use the 3-steps for factoring a cubic polynomial by grouping as follows:

 

Figure 09: Find the factors of the cubic polynomial 2x³ - 3x² + 18x - 27

 


Step One: Split the cubic polynomial into groups of two binomials.

After splitting this cubic polynomial, you end up with these two groups: (2x³ - 3x²) and (18x-27)

 

Figure 10: Step One: Split the cubic polynomial into two groups

 

Step Two: Factor each binomial by pulling out a GCF

Next, divide a GCF out of each group (if possible) as follows:

  • (2x³ - 3x²) → x²(2x - 3)

  • (18x - 27) → 9(2x - 3)

This process of pulling a GCF out of each group is illustrated in Figure 11 below:

 

Figure 11: Factorize a cubic polynomial

 

Step Three: Identify the factors

Since both factors have a common term, (2x-3), you know that you have likely factored correctly and you can move onto identifying the factors.

Final Answer: (x²+9) and (2x-3) are the factors of the cubic polynomial 2x³ - 3x² + 18x - 27.

All of the steps for solving Example #2 are illustrated in Figure 12 below.

 

Figure 12: The factors are (x²+9) and (2x-3)

 

Just like the last example, you can check to see if your final answer is correct by multiplying the factors together and seeing if the result equals the original cubic polynomial.

Example #3: Factor 3y³ + 18y² + y + 6

Finally, lets work through one more example where you have to factorize a cubic polynomial.

Step One: Split the cubic polynomial into groups of two binomials.

Again, the first step is to split the cubic polynomial down the middle into two binomials as shown in Figure 13 below.

 

Figure 13: Factoring a cubic polynomial by grouping.

 

As shown in Figure 13 above, splitting the polynomial down the middle leaves you with these two groups: (3y³ +18y²) and (y+6)

Remember that the whole point of splitting the cubic polynomial is to create two binomials that each have a GCF. But notice that the second binomial, (y+6), is not factorable because there is no GCF between +y and +6.

But, as previously mentioned, this doesn’t mean that you can not solve this problem further. In fact, the commutative property of addition allows you to swap the positions of the two middle terms (18y² and +y).

This extra step of swapping the two middle terms is illustrated in Figure 14 below.

 

Figure 14: Sometimes you have to swap the positions of the middle terms in order to factorize a cubic polynomial.

 

After swapping the positions of the middle terms, you can now apply the 3-step method to factoring the equivalent polynomial: 3y³ + y + 18y² + 6 (this new cubic polynomial is equivalent to the original because the commutative property of addition allows you to rearrange the terms without changing the value of the expression).

Now, you actually can split the new cubic polynomial into groups that can be factoring by dividing out a GCF: (3y³ + y) and (18y² + 6)

 

Figure 15: After swapping the positions of the middle terms, you can continue on with factoring the cubic polynomial.

 

Step Two: Factor each binomial by pulling out a GCF

As shown in Figure 15 above, you can factor each group by pulling out a GCF as follows:

  • (3y³ + y) → y(3y² + 1)

  • (18y² + 6) → 6(3y² + 1)

Step Three: Identify the factors

Finally, you can conclude that:

Final Answer: The factors are (y+6) and (3y² + 1)

The step-by-step process to solving this 3rd example are shown in Figure 16 below. Again, you can make sure that your final answer is correct by multiplying the factors together and verifying that their product is equivalent to the original cubic polynomial.

 

Figure 16: How to factorize a cubic polynomial when you have to swap the middle terms.

 

How to Factorize a Cubic Polynomial: Conclusion

It is beneficial to understand how to factorize a cubic polynomial because the skill will allow you to simplify and understand the behavior of cubic functions as you continue onto higher levels of algebra and begin to explore topics like finding roots, analyzing graphs, and solving cubic equations.

Factoring cubic functions can be challenging, but you can always use the following 3-step grouping method described in this guide to successfully factor a cubic polynomial (assuming that it is factorable in the first place):

Step One: Split the cubic polynomial into groups of two binomials.

Step Two: Factor each binomial by pulling out a GCF

Step Three: Identify the factors

Keep Learning:

1 Comment