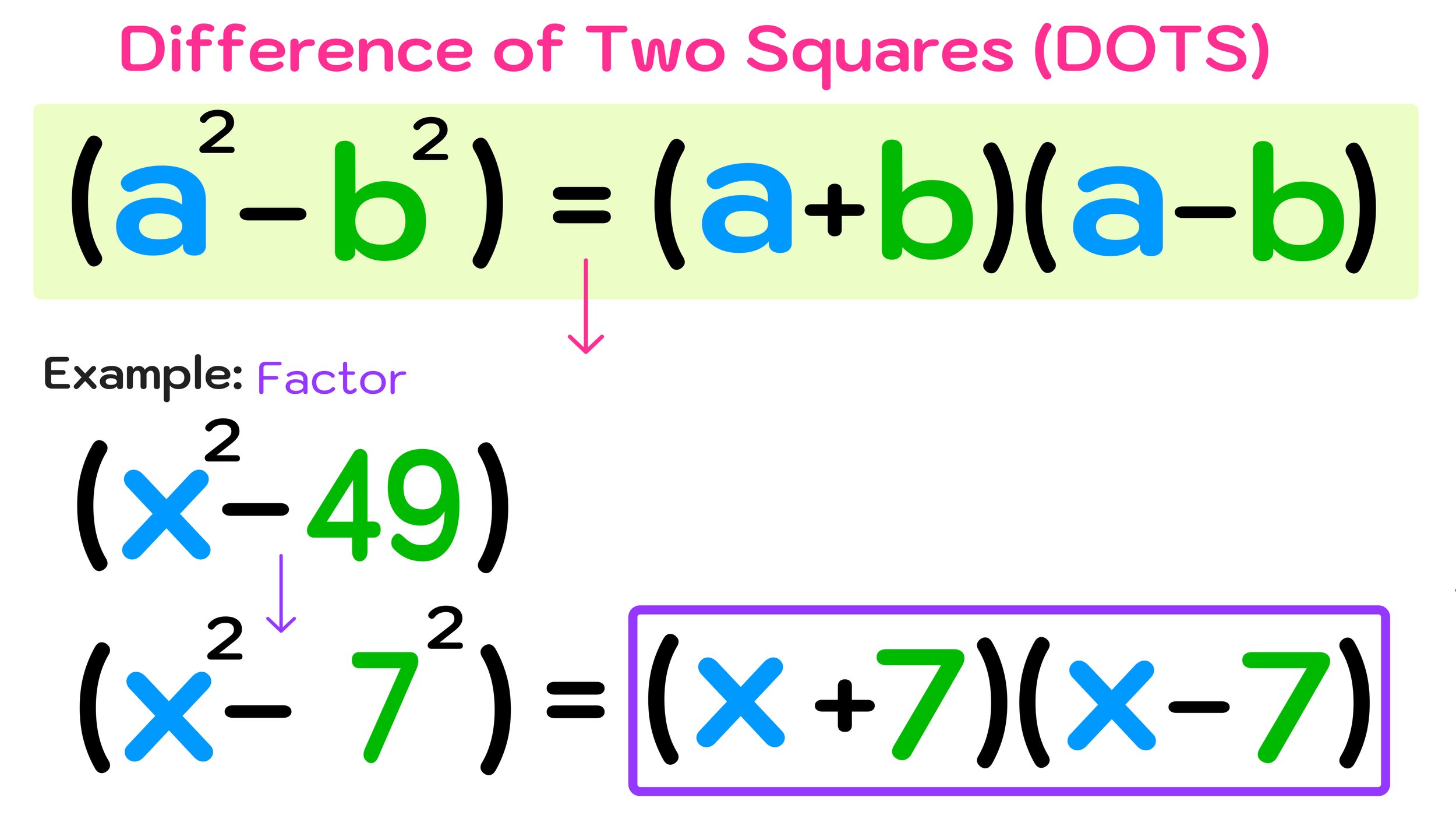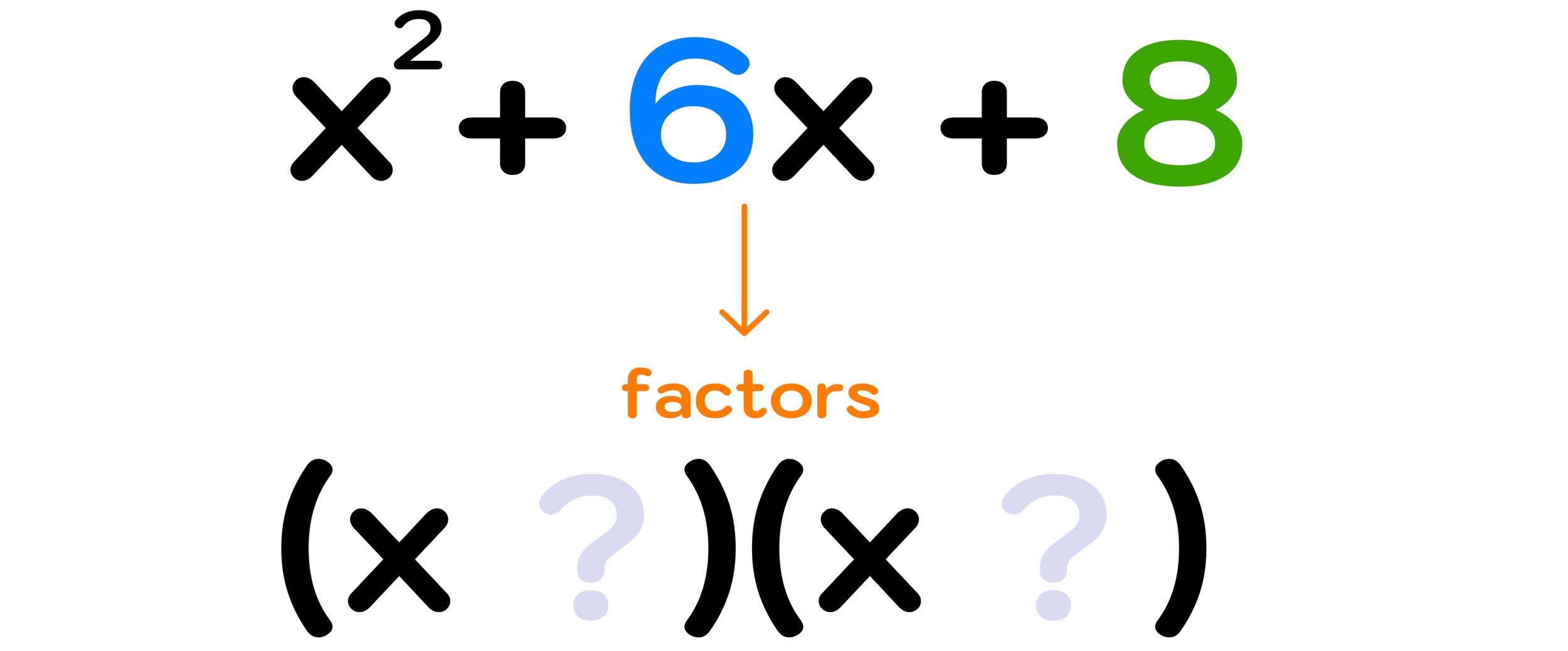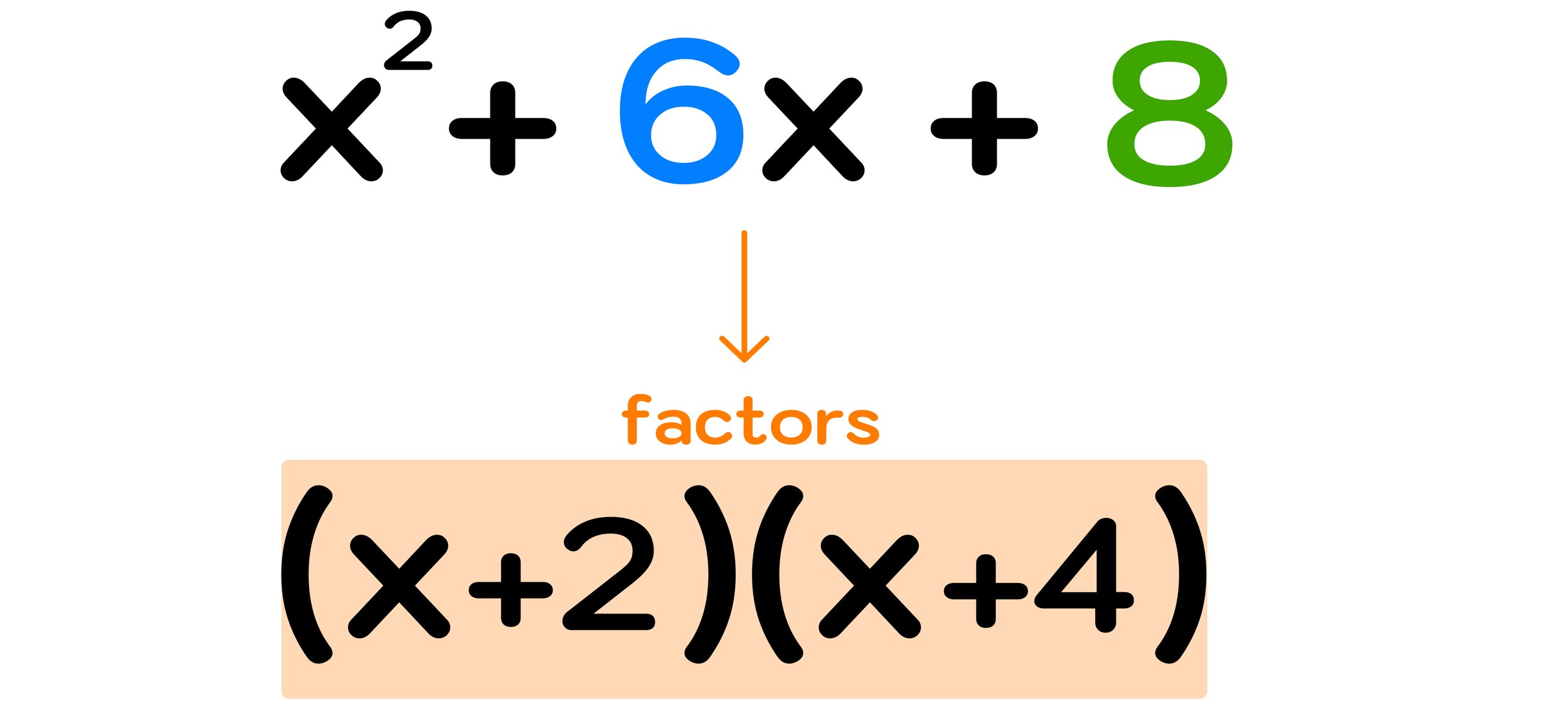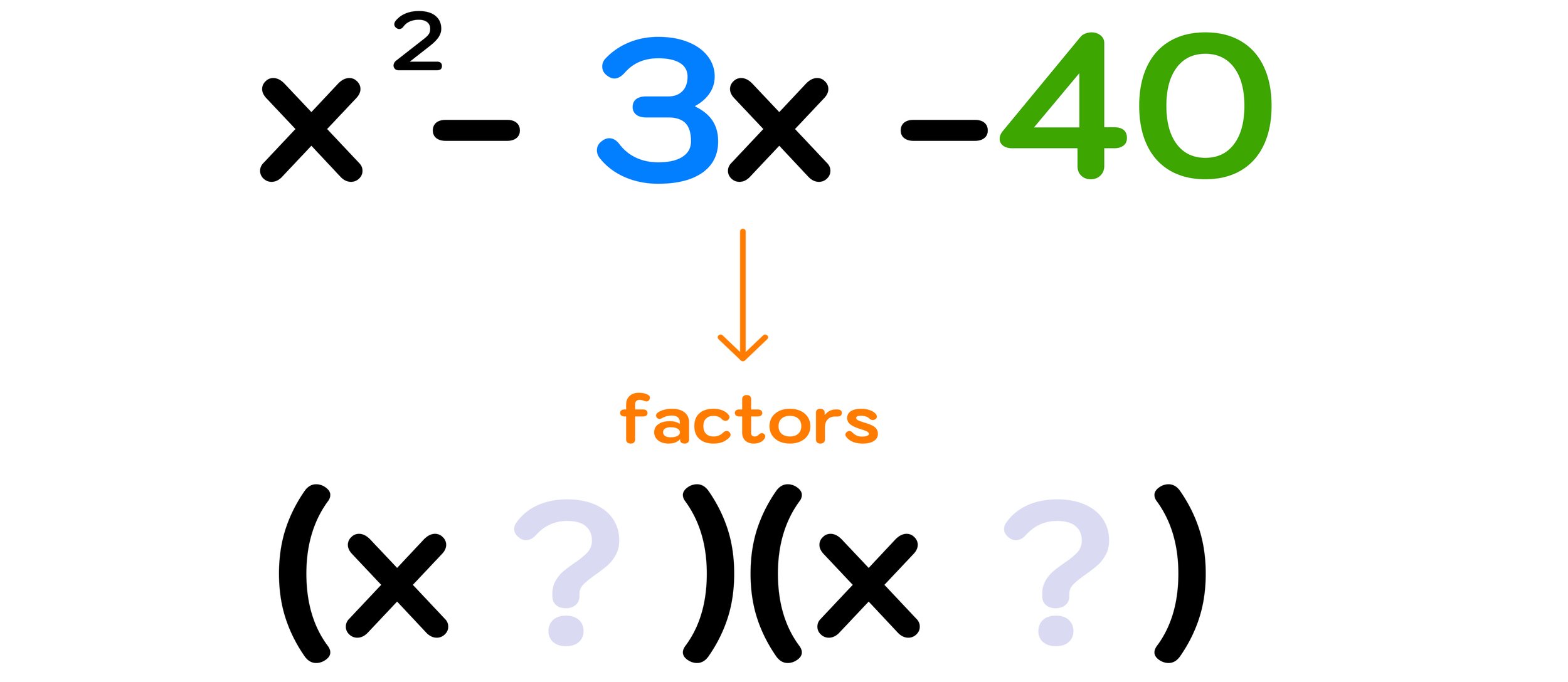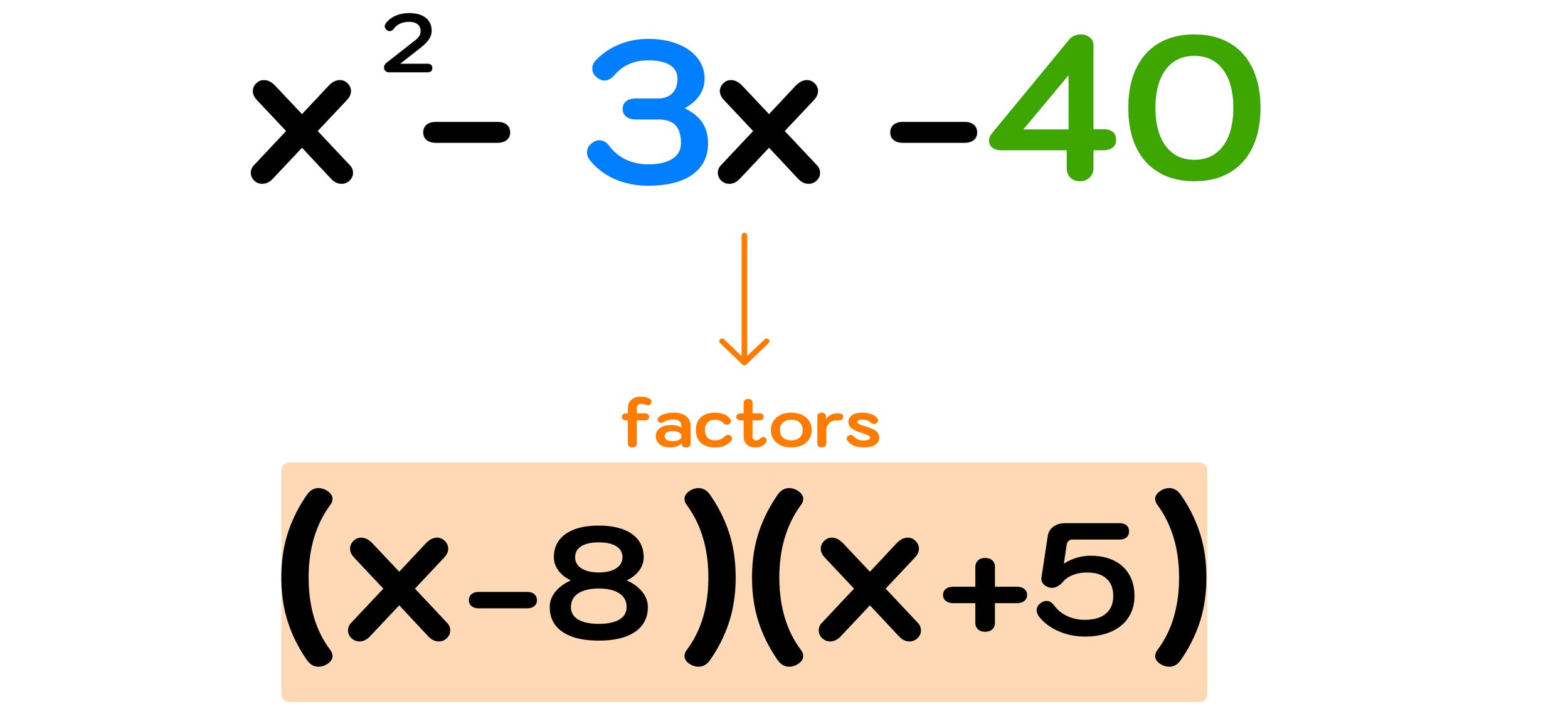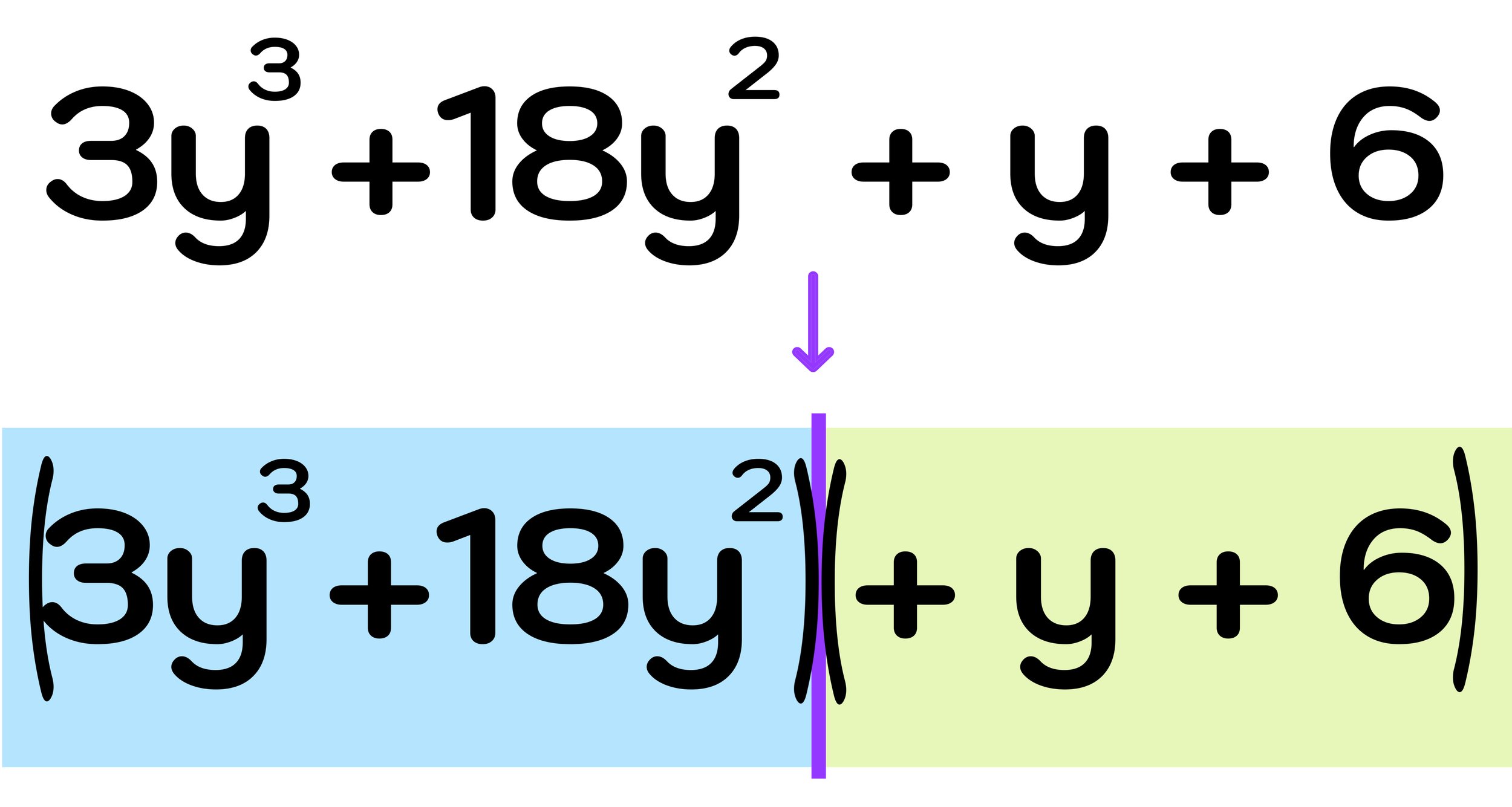Viewing entries tagged
how to factor a polynomial with 4 terms

How to Factor Polynomials—Step-by-Step Examples and Tutorial

How to Factor Polynomials—Step-by-Step Examples and Tutorial

How to Factor Polynomials Explained

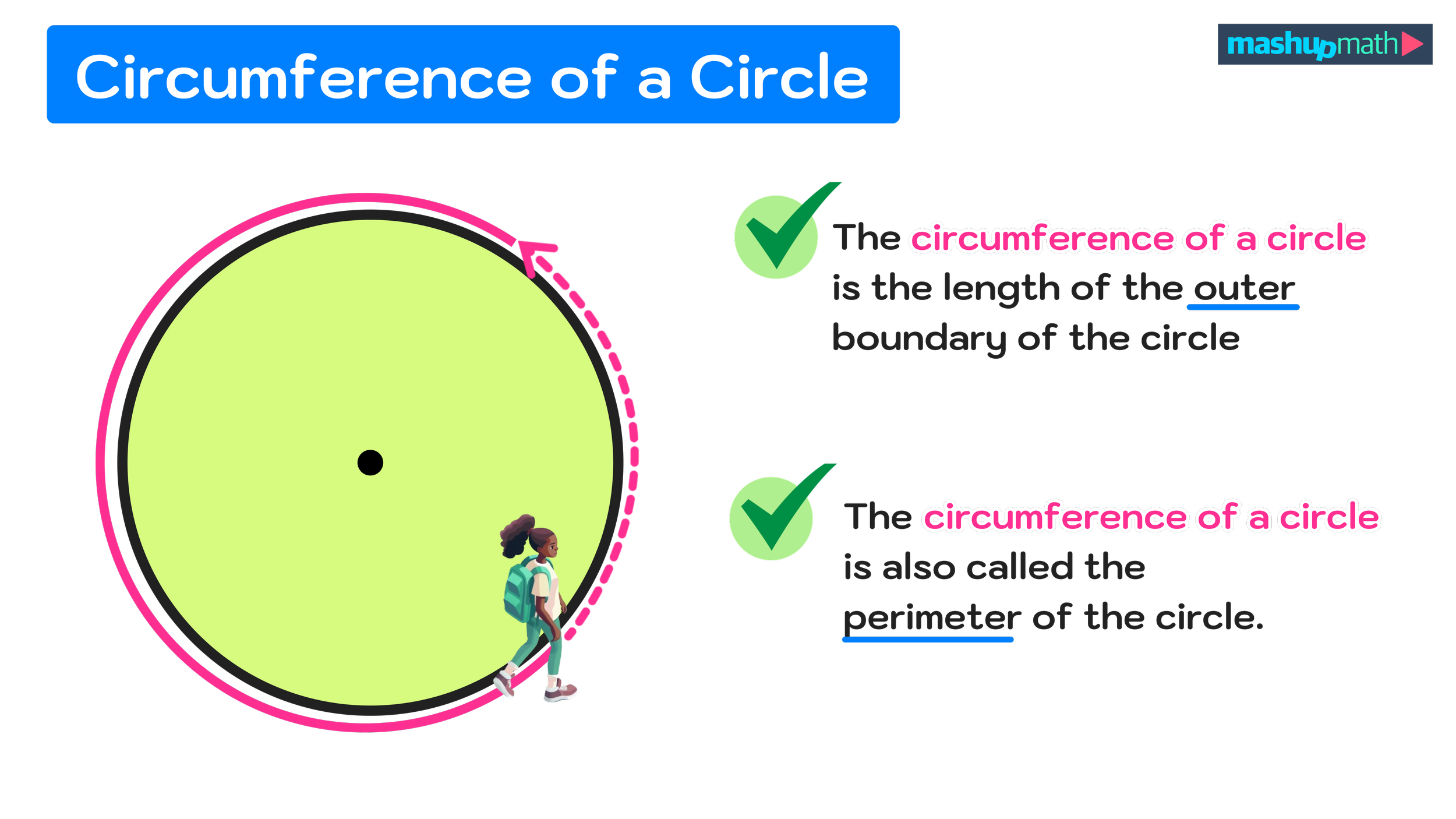
Factoring polynomials is a process of rewriting a polynomial as the product of one or more simpler expressions—including constants, variables, or factors that can not be further reduced. How to factor a given polynomial will depend on a few different factors, including the number of terms, the value of the coefficients, and the structure of the polynomial.

 

Free Step-by-Step Guide: How to factor a polynomial with a specific number of terms

 
Anthony Persico

by Anthony Persico

Founder & Head Educator, Mashup Math
With a background in elementary and secondary math education and special education, Anthony has taught thousands of K-12 students across the United States.

Learn more about the author →

Last Updated: May 2025

In algebra, a polynomial is an expression made up of variables and coefficients separated by the operations of addition and/or subtraction.

Polynomials are a fundamental math topic and understanding how to work with them (including factoring) is essential to being successful in algebra and beyond. Learning how to factor polynomials with 2, 3, or 4 terms involves understanding how to break down a given polynomial into simpler factors.

This free Step-by-Step Guide on How to Factor Polynomials will cover the following topics:

Table of Contents

While learning how to factor polynomials can be challenging, it is a learnable skill that can be acquired through practice. The goal of this free guide on how to factor polynomials is to give you plenty of step-by-step practice with factoring polynomials—including polynomials with 4 terms (cubic polynomials)—so that can become more comfortable with factoring all kinds of polynomials.

Before we cover everything you need to know about how to factor a polynomial, let’s quickly recap some key algebra vocabulary terms and phrases that you will need to be familiar with in order to use this guide.

 

Figure 01: How to Factor Polynomials: What is a Polynomial?

 

What is a polynomial?

As previously stated, a polynomial is a math expression comprised of variables, coefficients, and/or constants separated by the operations of addition or subtraction.

The terms of polynomials are individual parts, or monomials, separated by addition or subtraction signs.

For example,

  • 3x² is a monomial

  • 3x² + 6x is a polynomial with 2 terms (3x² and 6x)

  • 3x² + 6x - 15 is a polynomial with 3 terms (3x², 6x, and -15)

  • 9x³ + 3x² + 6x - 15 is a polynomial with 4 terms (9x³, 3x², 6x, and -15)

Figure 01 above illustrates the difference between a monomial and a polynomial.

For an expression to be considered a polynomial, it must have at least two terms, but there is no limit on how many terms a polynomial can have.

When it comes to factoring polynomials, you will most commonly be dealing with polynomials that have 2 terms, 3 terms, or 4 terms:

  • A polynomial with 2 terms is called a binomial

  • A polynomial with 3 terms is called a trinomial

  • A polynomial with 4 terms is called a quadrinomial (also known as a cubic polynomial)

Examples of a polynomial with 2 terms, 3 terms, and 4 terms are shown in Figure 02 below.

 

Figure 02: How to factor polynomials with 4 terms or less.

 

Now that you understand the key terms and the difference between a polynomial with 2 terms, 3 terms, and 4 terms.

For factoring each type of polynomial, we will look at two methods: GCF, direct factoring, and a combination of the two.

Let’s get started!

How to Factor Polynomials with 2 Terms

We will start by learning how to factor polynomials with 2 terms (binomials).

Whenever you are factoring a polynomial with any number of terms, it is always best to start by looking to see if there is a GCF—or greatest common factor—that all of the terms have in common.

For example, consider the following example:

Example #1: Factor 8x + 4

For this example, you should notice that both terms, 8x and 4 are divisible by 4, hence they share a GCF of 4.

Therefore, you can divide out the GCF of 4 from both terms as follows:

  • 8x + 4 → 4 (2x + 1)

So, the factors of 8x + 4 are: 4 and (2x+1).

What we just did was essentially the reverse of the distributive property, as shown in Figure 03 below.

 

Figure 03: How to factor a polynomial with 2 terms using the GCF method.

 

Note that many binomials can be factored using the GCF method, so let’s gain a little more practice with one more example (understanding how to simplify and/or factor a polynomial using the GCF method will come in handy when you start factoring 3 and 4 term polynomials later on).

Example #2: Factor 6x² + 12x

Just like the first example, there is a GCF for both terms. But, in this case, the GCF includes a variable. Why? Because both terms have coefficients that are divisible by 6 and both terms have at least one x variable, so the GCF, in this case, is 6x.

Therefore, you can divide out 6x from both terms as follows:

  • 6x² + 12x → 6x(x + 2)

So, the factors of 6x² + 12x are: 6x and (x+2).

Again, this method of factoring is just the reverse of the distributive property and is illustrated in Figure 04 below.

 

Figure 04: How to factor a polynomial with 2 terms using the GCF method.

 

Next, we will look at a special case of factoring a binomial—when the binomial is a difference of two squares (this is sometimes referred to as DOTS).

Whenever you have a binomial of the form a²-b², the factors will be of the form (a+b)(a-b).

Example #3: Factor x² - 49

For example, if you wanted to factor the binomial: x² - 49, you would notice that both x² and 49 are squares:

  • x² = (x)(x)

  • 49=(7)(7)

So, another way to write (x²- 49) is (x²- 7²)

Therefore, you can use the DOTS method for factoring binomials. In this case, a = x and b = 7, so:

  • (a²-b²) = (a+b)(a-b) → (x²- 7²) = (x-7)(x+7)

You can now conclude that the factors of x²- 49 are (x-7) and (x+7) using the DOTS method.

This process is illustrated in Figure 05 below:

 

Figure 05: How to factor a polynomial that is the difference of two squares.

 

If you want to learn more about the DOTS method for factoring polynomials that are the difference of two squares, check out this free video tutorial on YouTube for more practice.

And if you want more practice, check out our free Factoring Polynomials Worksheet Library, where you can download free PDF practice worksheets with answer keys.

Otherwise, let’s continue onto the next section where you will learn how to factor polynomials with 3 terms.

How to Factor Polynomials with 3 Terms

Moving on, we will now look at polynomials with 3 terms, typically referred to as trinomials

Learning how to factor polynomials with 3 terms involves a more involved factoring process that we will explore in this section.

The trinomials that we will cover will be of the form ax² + bx + c (where c is a constant). The strategies that we will use will depend on whether a (the leading coefficient) equals one or not. Therefore, the first two examples in this section will be factoring trinomials when a=1 and the second two examples will be when a≠1.

How to Factor Polynomials with 3 Terms when a=1

Example #1: Factor x² + 6x + 8

For the first example, we have to factor the trinomial: x² + 6x + 8

 

Figure 06: How to factor polynomials with 3 terms (when a=1)

 

Again, the leading coefficient, a, is equal to 1 in this example. This is important to note because the following method for factoring a trinomial only works when a=1.

Now we are ready to factor this trinomial in 3 easy steps:

Step One: Identify the values of b and c.

In this example, the values of b and c in the trinomial are: b=6 and c=8

Step Two: Figure out two numbers that both ADD to b and MULTIPLY to c.

The second step often involves some of trial-and-error as you pick numbers and see if they meet both conditions (the two numbers have to add together to make b and multiply together to make c).

  • 5 + 1 =6 (the value of b) ✓

  • 5 x 1 ≠ 8 (the value of c) ✘

For example, lets say that you chose the numbers 5 and 1. While 5+1=6 is true (satisfying the first condition), 5x1=5 (not 8), therefore, they do not satisfy the second condition. So, 5 and 1 do not work.

But, if you picked the numbers 2 and 4, you can see that:

  • 2 + 4 =6 (the value of b) ✓

  • 2 x 4 = 8 (the value of c) ✓

Since 2 and 4 satisfy both conditions, you can stop searching and move onto the third step.

Step Three: Use your numbers from step two to write out the factors

In this case, you can conclude that the factors of x² + 6x + 8 are (x+2) and (x+4).

 

Figure 07: The factors of x² + 6x + 8 are (x+2) and (x+4).

 

You can verify that these are the correct factors by performing double distribution as follows:

  • (x+2)(x+4) = x² + 2x + 4x + 8 = x² + 6x + 8

Notice that you ended up with the trinomial that you started with! Now, lets work through one more example of how to factor polynomials with 3 terms when a=1.

Example #2: Factor x² - 3x - 40

For this next example, we have to factor the trinomial: x² - 3x - 40

 

Figure 08: How to factor 3rd degree polynomials

 

Notice that, in this case, the trinomial includes subtraction signs, which will affect how you perform step two below.

Step One: Identify the values of b and c.

For this trinomial, b= -3 and c= -40

Step Two: Figure out two numbers that both ADD to b and MULTIPLY to c.

Again, you have to find two numbers that add to make -3 and that multiply together to make -40.

This part can be tricky when both of the values for b and c are negative (like in this example). You have to recall that a negative number times another negative number will lead to a positive result, so you can’t have two negatives (since you need to find two numbers that multiply together to make -40).

Eventually, after some trial-and-error, you should find that -8 and +5 satisfy both conditions:

  • -8 + 5 =-3 (the value of b) ✓

  • -8 x 5 = -40 (the value of c) ✓

Step Three: Use your numbers from step two to write out the factors

Finally, you can conclude that the factors of x² - 3x -40 are (x-8) and (x+5).

(You make sure that this answer is correct, you can perform double distribution on (x-8)(x+5) to make sure that the result is equal to the original trinomial).

 

Figure 09: The factors of x² - 3x -40 are (x-8) and (x+5).

 

If you want more practice factoring trinomials when a=1, check out our free step-by-step guide on how to factor trinomials to gain some more practice.

And if you want more independent practice opportunities, check out our free Factoring Polynomials Worksheet Library, where you can download free PDF practice worksheets with answer keys.

Otherwise, you can continue on to learn how to factor polynomials with 3 terms when a≠1.

How to Factor Polynomials with 3 Terms when a≠1

Example #1: Factor 2x² - x - 6

For the first example, we have to factor the trinomial: 2x² - x - 6

 

Figure 10: How to factor polynomials with 3 terms when a≠1

 

For starters, notice that you can not pull out a GCF.

So, to solve trinomials of the form ax² + bx + c when a≠1, you can use the AC method as follows:

Step One: Identify the values of a and c and multiply them together

In this case, a=2 and c=-6, so

  • a x c = 2 x -6 = -12

Step Two: Factor and replace the middle term

The second step requires you to use the result from step one to factor and replace the middle term.

The middle term is currently -1x and note that:

  • -12 = -4 x 3; and

  • -4 + 3 = -1

We chose -4 and 3 as factors because the sum of -4 and 3 equals negative 1, so we can rewrite the original trinomial as 2x² - 4x +3x - 6

 

Figure 11: Factor and replace the middle term

 

Step Three: Split the new polynomial down the middle and take the GCF of each side

Note that we are now working with a polynomial that actually has four terms: 2x² - 4x + 3x - 6

In this third step, you have to split the polynomial down the middle to essentially create two separate binomials that you can simplify by dividing GCF’s out of as follows:

  • First Half: 2x² - 4x = 2x(x-2)

  • Second Half: 3x - 6 = 3(x-2)

This third step is illustrated in Figure 12 below:

 

Figure 12: Split the new polynomial down the middle and take the GCF of each side

 

Step Four: Identify the Factors

Finally, you are ready to identify the factors.

The result from the previous step was 2x(x - 2) + 3(x -2). Hidden within this expression are your two factors, which you can see by looking at Figure 13 below.

 

Figure 13: The final step is to identify the factors

 

Finally, you can conclude that the factors of 2x² - x - 6 are (2x+3) and (x-2).

Clearly, factoring a trinomial when a≠1 can be a tricky and there are several steps along the way, but, the more that you practice this process, the better you will become at factoring polynomials with 3 terms like the one in this past example. To give you a little more practice, lets work through one more example before we move on to learning how to factor cubic polynomials.

Example #2: Factor 4x² - 15x + 9

 

Figure 14: Factor the trinomial where a=4, b=-15, and c=9

 

Step One: Identify the values of a and c and multiply them together

In this example, a=4 and c=9, so

  • a x c = 4 x 9 = 36

Step Two: Factor and replace the middle term

For the next step, note that the middle term is -15x, so you will need to find two numbers that multiply to 36 and add to -15:

  • 36 = -12 x -3; and

  • -12 + -3 = -15

Now, we can rewrite the original trinomial as 4x² -12x -3x +9

Step Three: Split the new polynomial down the middle and take the GCF of each side

For step three, you have to split the polynomial into two separate binomials and divide a GCF out of each one as follows:

  • First Half: 4x² -12x = 4x(x-3)

  • Second Half: -3x+9 -3(x-3)

Step Four: Identify the Factors

The last step is to identify the factors as shown in Figure 15 below.

 

Figure 15: The factors are (4x-3)(x-3)

 

Now, you can conclude that the factors of 4x² - 15x + 9 are (4x-3) and (x-3).

You can again use double distribution on (4x-3)(x-3) to verify that your solution is correct.

If you need more step-by-step help with how to factor polynomials with 3 terms when a does not equal 1, visit out our free Factoring Polynomials Worksheet Library, where you can download free PDF practice worksheets with answer keys.

Otherwise, continue on to the final section where you will learn how to factor polynomials with 4 terms.

How to Factor Polynomials with 4 Terms

The last section of this guide will cover how to factor polynomials with 4 terms and how to factor cubic polynomials.

In this section, we are going to apply a grouping method for how to factor a cubic polynomial that is very similar to the way that you factored trinomials when the leading coefficient, a, did not equal one in the last section. So, you may want to review that section before moving onto the 4 term polynomial factoring examples, however, it is not completely necessary, as we will be taking a step-by-step approach to solving two examples of factoring cubic polynomials.

Now, lets go ahead and work through our first example on how to factor cubic polynomials.

 

Figure 16: Polynomials with 4 terms are referred to as cubic polynomials.

 

Example #1: Factor 2x³ - 3x² + 18x - 27

For the first example, we have to factor the cubic polynomial: 2x³ - 3x² + 18x - 27

Step One: Split the cubic polynomial into groups of two binomials.

To factor this 4 term polynomial, we are going to apply what is called the grouping method, which requires you to split the polynomial into two groups (two separate binomials) with the goal of factoring a GCF out of each one.

 

Figure 17: How to Factor Cubic Polynomials by Grouping: The first step is to split the polynomial into two groups of binomials.

 

Remember that the goal is to create two separate binomials that have a GCF. If there is no apparent GCF, you have the option of swapping the positions of the middle terms (- 3x² and 18x), but that is not necessary for factoring this 4 term polynomial.

In this example, by the end of step one, you now have two groups to factor:

  • (2x³ - 3x²)

  • (18x - 27)

Step Two: Factor each binomial by pulling out a GCF

Now, go ahead and divide a GCF out of each binomial as follows:

  • (2x³ - 3x²) → x²(2x - 3)

  • (18x - 27) → 9(2x - 3)

This step is illustrated in Figure 18 below.

 

Figure 18: How to factor a cubic polynomial by grouping.

 

Step Three: Identify the factors

Notice that both results have a (2x-3) term. This is important and expected. If both results do not share a same term, then you either made a mistake or the polynomial with 4 terms is not factorable.

But, since we were able to factor each group by pulling out a GCF that resulted in both groups sharing a common factor of (2x-3), we know that we can factor out the other terms (x² and +9), so now have our factors: (x²+9) and (2x-3)

Final Answer: The factors of 2x³ - 3x² + 18x - 27 are (x²+9) and (2x-3)

The entire process of how to factor polynomials by 4 terms by grouping is illustrated in Figure 19 below.

 

Figure 19: The factors of 2x³ - 3x² + 18x - 27 are (x²+9) and (2x-3)

 

Example #2: Factor 3y³ + 18y² + y + 6

Let’s gain some more practice with how to factor a cubic polynomial by grouping by solving one more example problem.

In this case, we have to factor the cubic polynomial 3y³ + 18y² + y + 6 using the same grouping method as the previous example.

Step One: Split the cubic polynomial into groups of two binomials.

Start by splitting the cubic polynomial into two groups (two separate binomials).

 

Figure 20: Split the cubic polynomial into two groups of binomials and check to see if they can both be factored by pulling out a GCF.

 

As shown in Figure 20 above, by completing step one, you are left with these two groups

  • (3y³ +18y²)

  • (y+6)

Hold on! Before moving onto the next step, you should notice that the second group (y+6) cannot be factored by pulling out a GCF (because there is no greatest common factor between 1y and 6).

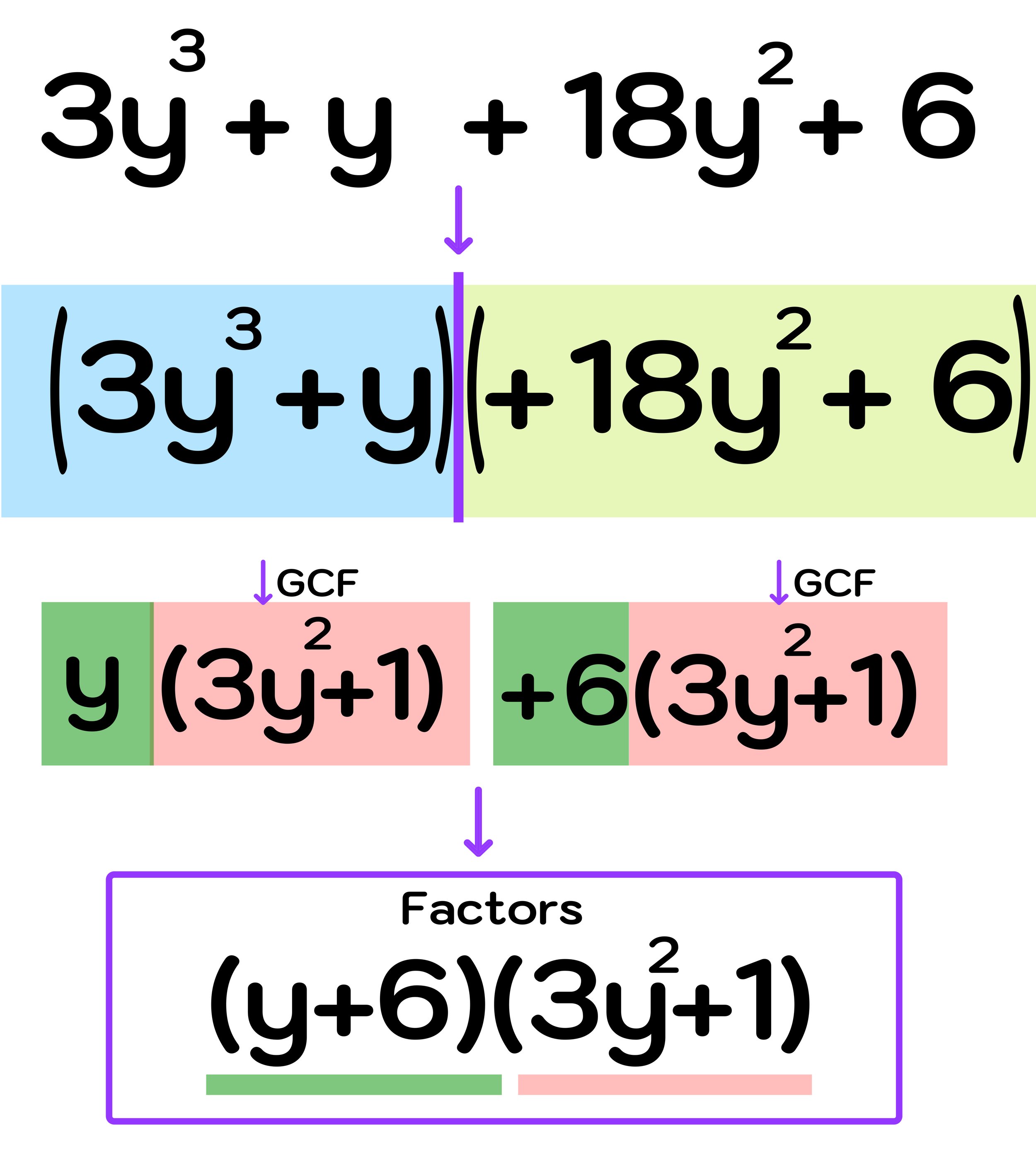
However, notice that we can swap the middle terms of the cubic polynomial (18y² and +y) as shown in Figure 21 below.

Now, we can factor a new 4 term polynomial 3y³ + y + 18y² + 6 that is equivalent to the original 4 term polynomial since the commutative property of addition allows you to rearrange the terms.

 

Figure 21: The commutative property of addition allows you to rearrange the middle terms when you are unable to group and GCF the original cubic polynomial.

 

Notice that you can split this new polynomial into two binomials that can be factored by pulling out a GCF:

  • (3y³ + y)

  • (18y² + 6)

 

Figure 22: After rearranging the original cubic polynomial, you can split it into two binomial groups that can be factoring by pulling out a GCF.

 

Step Two: Factor each binomial by pulling out a GCF

As illustrated in Figure 22 above, after rearranging the original cubic polynomial, you can split it into two binomial groups that can be factoring by pulling out a GCF as follows:

  • (3y³ + y) → y(3y² + 1)

  • (18y² + 6) → 6(3y² + 1)

Step Three: Identify the factors

Now, you can see that both factors have a (3y² + 1) term, which means that you have factored correctly.

Final Answer: The factors of 3y³ + 18y² + y + 6 are (y+6) and (3y² + 1)

The entire process of how to factor polynomials a cubic polynomial like the one in this example is illustrated in Figure 23 below.

 

Figure 23: How to factor cubic polynomials by grouping (step-by-step).

 

Factoring Polynomials Advanced Problems

Now that we have covered how to factor polynomials in a variety of different ways, let’s take a look at two advanced factoring polynomials problems. These are the type of questions that you might find on a unit test or a standardized exam. Let’s see if we can apply what we learned earlier in this guide to solve it.

Advanced Factoring Polynomials Problem #1

Factor: (2/3)x² + (1/3)x -1

At first glance, this factoring problem looks different than our previous examples because it has fractions as coefficients. However, since the polynomial is in ax² +bx + c form, we can factor it using a familiar strategy.

First, let’s identify the values of a, b, and c:

  • a= 2/3

  • b=1/3

  • c=-1

Since 2/3, 1/3, and 1 do not share any common factors, we can not pull out a GCF.

Figure 24: Factoring Polynomials Advanced Problem #1

But, we can use the AC method to factor this trinomial as follows:

Step One: Identify the values of a and c and multiply them together

In this case, a=2/3 and c= -1, so

  • a x c = 2/3 x -1 = (-2/3)x

Step Two: Factor and replace the middle term

For the next step, we have to use our result from step one to factor and replace the middle term (1/3)x:

The middle term is currently -1x and note that:

  • (1/3)x = (-2/3)x + 1x

Since our current middle term ((1/3)x is equivalent to (-2/3)x + 1x, we can rewrite the original trinomial as:

  • (2/3)x² - (2/3)x + 1x -1

Step Three: Split the new polynomial down the middle and take the GCF of each side

For the third step in the AC method, we have to split the polynomial down the middle and take the GCF of each side:

  • First Half: (2/3)x² - (2/3)x

  • Second Half: 1x -1

After taking out the GCF, we are left with:

  • First Half: (2/3)x² - (2/3)x → (2/3)x(x-1)

  • Second Half: 1x -1 → +1(x-1)

Step Four: Identify the Factors

Finally, you just have to identify the factors, which are ((2/3)x+1)(x-1)

Final Answer: (2/3)x² + (1/3)x -1 = ((2/3)x+1)(x-1)

The entire step-by-step process for solving this problem is shown in Figure 24.

 

Advanced Factoring Polynomials Problem #2

Factor: x³ -3x² -4x + 12

We can factor this cubic polynomial by grouping:

  • (x³ -3x²) + (-4x + 12)

Next, we have to factor each separate group:

  • (x³ -3x²) → x²(x-3)

  • (-4x + 12) → -4(x-3)

Now, we can factor out (x-3), and rewrite the result as:

  • (x²-4)(x-3)

While this may look like a final answer, we should notice that (x²-4) is a difference of two squares that we can factor as:

  • (x²-4) = (x+2)(x-2)

Finally, we can conclude that:

Final Answer: x³ -3x² -4x + 12 = (x-3)(x+2)(x-2)

Free Factoring Polynomials Practice Worksheets

If you want to further test your understanding of factoring polynomials, including the difference of two squares, factoring trinomials, factoring by completing the square, and factoring polynomials by grouping, then visit the Mashup Math Factoring Polynomials Worksheet Library, where you can download several free PDF practice worksheets with complete answer keys.

Click here to access our free Factoring Polynomials Worksheet Library.

How to Factor Polynomials: Conclusion

Learning how to factor a polynomial is an important algebra skill that every math student must learn at some point.

While factoring polynomials can be tricky, there are several useful and effective strategies that you can use to factor polynomials. The strategy that you choose will depend on how many terms a polynomial has (as you will often be dealing with factoring polynomials with 2, 3, or 4 terms).

The best way to get better at factoring polynomials (especially cubic polynomials that have 4 terms) is by working through practice problems step-by-step. If you feel like you need more practice, we highly recommend working through the examples in this guide several times to gain more experience.

Keep Learning:

Quadratic Formula Examples—Solved Step-by-Step

Comment

Quadratic Formula Examples—Solved Step-by-Step

Quadratic Formula Examples Tutorial

Step-by-Step Guide: Examples of How to Find the Roots of a Quadratic Function using the Quadratic Formula

 

Step-by-Step Guide: Quadratic Formula Examples Solved

 

Are you ready to work through a few quadratic formula examples to gain some more practice and experience with solving quadratic equations using the quadratic formula?

In math, the quadratic formula, x= (-b ± [√(b² - 4ac)]) / 2a is an incredibly important and useful formula that you can use to find the solutions (also known as roots) or any quadratic equation of the form ax² + bx + c = 0 (where a ≠ 0), whether it is easy to factor or not!

If you know how to use the quadratic formula, then you can solve a variety of algebra problems involving quadratic equations, and learning how to use it correctly is something that you can easily learn with some practice and repetition.

This free Quadratic Formula Examples Step-by-Step Guide includes a short review of the quadratic formula as well as several different practice problems that we will work through and solve using the quadratic formula with a step-by-step explanation. The guide is organize by the following sections, and you can click on any of the hyperlinks below to jump to any particular spot:

Before we dive into any of the quadratic formula examples, let’s start off with a quick review of the quadratic formula and why it is such a useful algebra tool.

 

Figure 01: The Quadratic Formula

 

What is the Quadratic Formula?

Before you can learn how to use the quadratic formula, it is important that you understand what a quadratic equation is.

Definition: A quadratic equation is a function of the form ax² + bx + c = 0 (where a does not equal zero). On a graph, a quadratic equation can be represented by a parabola. The x-values where the parabola crosses the x-axis is called the solutions, or roots, of the quadratic equation.

For example, consider the following quadratic equation:

  • x² + 5x + 6 = 0

Notice that this equation is in ax² + bx + c = 0 form, where…

  • a=1

  • b=5

  • c=6

If we want to find the solutions, or roots, of this quadratic equation, we have a few options.

First, we could factor this quadratic equation by looking for two values that add to 5 and also multiply to 6, which, in this case, would be 2 and 3. So we could say that…

  • x² + 5x + 6 = 0 → (x+2)(x+3) = 0

We could then solve for each factor as follows:

  • x + 2 = 0 → x = -2

  • x + 3 = 0 → x = -3

Now we can conclude that the solutions of this quadratic are x=-2 or x=-3.

 

Figure 02: What are the solutions (or roots) of a quadratic equation?

 

Another option for finding the solutions to a quadratic equation is to look at its graph. The solutions, or roots, will be the x-values where the graph crosses the x—axis. Note that quadratic equations can have two roots, one root, or even no real roots (as you will see later in this guide).

As for the equation x² + 5x + 6 = 0, the corresponding graph in Figure 02 above confirms that the equation has solutions at x=-2 and x=-3.

But what do we do when a quadratic equation is very difficult to factor or when we do not have access to a clear graph? Well, this is where the quadratic formula comes into play.

Definition: Any quadratic equation of the form ax² + bx + c = 0 (where a ≠ 0), can be solved using the quadratic formula, which states that…

  • x= (-b ± [√(b² - 4ac)]) / 2a

Why is the quadratic formula so useful? Because, as the definition states, it can be used to find the solutions to any quadratic equation. While the quadratic equation that we just looked at, x² + 5x + 6 = 0, was pretty easy to work with and solve, it is considered extremely simple. As you move farther along your algebra journey, you will come across more and more complex quadratic equations that can be very difficult to factor or even graph.

However, if you know how to use the quadratic formula, you can successfully solve any quadratic equation. With this in mind, let’s go ahead and work through some quadratic formula examples so you can gain some practice.

And we will start by using it to solve x² + 5x + 6 = 0, because we already know that the solutions are x=-2 and x=-3. If the quadratic formula works, then it should yield us that same result. Once we work through this first simple example, we will move onto more complex examples of how to use the quadratic formula to solve quadratic equations.

 

Figure 03: To use the quadratic formula, start by identifying the values of a, b, and c.

 

Quadratic Formula Examples

We will begin by using the quadratic formula to solve the equation shown in Figure 02 above: x² + 5x + 6 = 0

Example #1: Solve x² + 5x + 6 = 0

First, notice that our equation is in ax² + bx + c = 0 form where:

  • a=1

  • b=5

  • c=6

Identifying the values of a, b, and c will always be the first step (provided that the equation is already in ax² + bx + c = 0 form).

Now that we know the values of a, b, and c, we can plug them into the quadratic equation as follows:

  • x= (-b ± [√(b² - 4ac)]) / 2a

  • x= -(5) ± [√(5² - 4(1)(6))]) / 2(1)

  • x= -5 ± [√(25 - 24)] / 2

  • x= -5 ± [√(1)] / 2

  • x= (-5 ± 1) / 2

Now we are left with x= (-5 ± 1) / 2. Note that the ± mean “plus or minus” meaning that we have to split this result into two separate equations:

  • Plus: x = (-5 + 1) / 2

  • Minus: x = (-5 - 1) / 2

By solving these two separate equations, we can find the solutions to the quadratic function x² + 5x + 6 = 0.

  • x = (-5 + 1) / 2 = -4/2 = -2 → x=-2

  • x = (-5 - 1) / 2 = -6/2 = -3 → x=-3

After solving both equations, we are left with x=-2 and x=-3, which we already knew were the solutions to x² + 5x + 6 = 0. So, we have confirmed that the quadratic formula can be used to find the solutions to any quadratic equation of the form ax² + bx + c = 0.

Final Answer: x=-2 and x=-3

The steps to solving the quadratic formula example is illustrated in Figure 04 below.

 

Figure 04: Quadratic Formula Examples Step-by-Step

 

Example #2: Solve 2x² + 2x -12 = 0

For our next quadratic formula example, we will again start by identifying the values of a, b, and c as follows:

  • a=2

  • b=2

  • c=-12

Make sure that you correctly identify the sign (positive or negative) as well, since this is necessary to using to quadratic formula correctly.

Next, we can substitute these values for a, b, and c into the quadratic formula as follows:

  • x= (-b ± [√(b² - 4ac)]) / 2a

  • x= -(2) ± [√(2² - 4(2)(-12))]) / 2(2)

  • x= -2 ± [√(4 - -96)] / 4

  • x= -2 ± [√(100)] / 4

  • x= (-2 ± 10) / 4

Our result is x= (-2 ± 10) / 4. From here, we can rewrite e the result as two separate equations by “spitting” the ± sign as follows:

  • Plus: x= (-2 + 10) / 4

  • Minus:x= (-2 - 10) / 4

Now we can solve each individual equation to find the values of x that will be the solutions of this quadratic equation.

  • x= (-2 + 10) / 4 = 8/4 = 2 → x=2

  • x = (-2 - 10) / 4 = -12/4 = 3 → x=3

We are left with two values for x: x=2 and x=-3, and we can conclude that the quadratic equation 2x² + 2x -12 = 0 has the following solutions:

Final Answer: x=2 and x=-3

Figure 05 shows the step-by-step process for solving this quadratic formula example.

 

Figure 05: Quadratic Formula Examples #2 Solved

 

Example #3: Solve 2x² -5x + 3 = 0

For the next of our quadratic formula examples calls for us to use the quadratic formula to find the solutions to a quadratic function where:

  • a=2

  • b=-5

  • c=3

The process of substituting a, b, and c into quadratic formula will be exactly the same as the last two quadratic formula examples.

  • x= (-b ± [√(b² - 4ac)]) / 2a

  • x= -(-5) ± [√(-5² - 4(2)(3))]) / 2(2)

  • x= 5 ± [√(25 - 24)] / 4

  • x= 5 ± [√(1)] / 4

  • x= (5 ± 1) / 4

Are you starting to get the hang of it? Now that we have simplified our equation, we are left with x= (5 ± 1) / 4. And, just like the last two examples, we can go ahead and split this result into two separate equations as follows:

  • Plus: x= (5 + 1) / 4

  • Minus: x= (5 - 1) / 4

Finally, we just have to solve each equation to get our final answer (i.e. the values of the solutions).

  • x= (5+1) / 4 = 6/4 = 3/2 → x=3/2

  • x= (5-1) / 4 = 4/4 = 1 → x=1

Notice that the result of the first equation ended up as a fraction (3/2). This is totally fine! It just means that the parabola will cross the x-axis in the middle of a box (rather than hitting directly at an integer coordinate).

Final Answer: x=3/2 and x=1

All of the steps for solving this example are shown in Figure 06 below.

 

Figure 06: Sometimes a quadratic formula will give you a solution that is a fraction.

 

Example #4: Solve 3x² + 2 = 7x

The fourth and final of our quadratic formula examples looks a bit different. The given equation 3x² + 2 = 7x is not in ax² + bx + c = 0 form.

Whenever this is the case, we will have to see if we can use algebra to rearrange the equation so to make into ax² + bx + c = 0 form. We can do that by using inverse operations to move the 7x to the left-side of the equation as follows:

  • 3x² + 2 = 7x

  • 3x² + 2 (-7x) = 7x (-7x)

  • 3x² + 2 -7x = 0

Notice that result, 3x² + 2 -7x = 0, still isn’t in ax² + bx + c = 0 form. However, the commutative property allows us to rearrange the terms as follows:

  • 3x² + 2 -7x = → 3x² -7x +2

Now we have an equivalent equation, 3x² -7x +2=0, that is in ax² + bx + c = 0 form, where:

  • a=3

  • b=-7

  • c=2

Sometimes you will be given equations that have to be rearranged in order to use the quadratic formula. If you can not rearrange an equation so that it can be expressed in ax² + bx + c = 0 form, then you can not solve it using the quadratic formula.

This example, however, can now be solved using the quadratic formula as follows:

  • x= (-b ± [√(b² - 4ac)]) / 2a

  • x= -(-7) ± [√(-7² - 4(3)(2))]) / 2(3)

  • x= 7 ± [√(49 - 24)] / 6

  • x= 7 ± [√(25)] / 6

  • x= (7 ± 5) / 6

Now we are left with a much easier equation to work with: x= (7 ± 5) / 6. Let’s go ahead and split it into two separate equations to solve it:

  • Plus: x= (7 + 5) / 6

  • Minus: x= (7 - 5) / 6

We can solve for x in each equation as follows:

  • x= (7+5) / 6 = 12/6 = 2 → x=2

  • x= (7-5) / 6 = 2/6 = 1/3 → x=1/3

Final Answer: x=2 and x=1/3

That’s all that there is to it! You can review of the steps to solving this quadratic formula example by looking at the illustration in Figure 07 below.

 

Figure 07: Quadratic Formula Examples: Rearranging an equation to put it into ax² + bx + c = 0 form.

 

Do you need more practice with using the Quadratic Formula?

Check out our free library of Quadratic Formula Worksheets (with answer keys)

Keep Learning:

Comment

How to Complete the Square in 3 Easy Steps

Comment

How to Complete the Square in 3 Easy Steps

How to Complete the Square in 3 Easy Steps

Step-by-Step Guide: How to do Completing the Square

 

Step-by-Step Guide: How to Complete the Square Explained.

 

As you continue onto more advanced problems where you have to factor quadratics, you will have to learn how to complete the square in order to find correct solutions. Completing the square is a special technique that you can use to factor quadratic functions.

This free step-by-step guide on How to Complete the Square will teach you an easy 3-step method for factoring any quadratic using a technique called “completing the square.”

This guide will focus on the following topics and sections. You can click on any of the text links below to jump to one particular section, or you can follow each section in sequential order.

Let’s begin by exploring the meaning of completing the square and when you can use it to help you to factor a quadratic function.

 

Figure 01: Are you ready to learn how to find solutions to quadratic equations by completing the square?

 

What is Completing the Square?

Completing the square is a method that you can use to solve quadratic equations of the form ax² + bx + c = 0 (where a, b, and c are all not equal to zero).

❗Note that the equations of the form ax² + bx + c = 0 are called quadratic equations and they can be rewritten as follows:

  • ax² + bx + c = 0

  • ax² + bx = -c

Both of these equations are equivalent to each other, and understanding the relationship between these two equations will help you to understand how to complete the square later on in this guide.

In the next section, we will work through three examples of how to complete the square using the following 3-step method:

  • Step #1: Rearrange the quadratic equation so that all of the constants are on one side of the equals sign.

  • Step #2: Add (b/2)² to both sides of the equal sign.

  • Step #3: Factor and solve.

By solving a quadratic equation by completing the square, you are identifying values where the parabola that represents the equation crosses the x-axis.

As long as you understand how to follow and apply these three steps, you will be able to solve quadratics by completing the square (provided that they are solvable). Now, let’s gain some experience with using the three step method on how to complete the square by working through some step-by-step practice problems.

 

Figure 02: The solutions to a quadratic equation are the values where the graph crosses the x-axis.

 

How to Complete the Square: Example #1

Solve: x² - 6x -16 = 0

For this first example (and all of the practice problems in this guide), we can solve the problem by completing the square using our three step method as follows:

Step #1: Rearrange the quadratic equation so that all of the constants are on one side of the equals sign.

Let’s start off by noticing that our given quadratic function is indeed in ax² +bx + c = 0 form, where a=1, b=-6, and c=-16.

To complete the first step, we have to move all of the constants (all of the values not attached to variables, to the right side of the equals sign as follows:

  • x² - 6x -16 = 0

  • x² - 6x -16 (+16) = 0 (+16)

  • x² - 6x = 16

Now we have completed the first step and we are left with a new equivalent equation:

  • x² - 6x = 16

Step #2: Add (b/2)² to both sides of the equal sign.

For the next step, we have to find the value of (b/2)² and add it to both sides of the equals sign.

Since we know that b=-6, we can find the value of (b/2)² by substituting -6 for b as follows:

  • (b/2)²

  • (-6/2)²

  • (-3)²

  • =9

In this case, (b/2)² = 9, so, to complete Step #2, we simply have to add 9 to both sides of the equal sign as follows:

  • x² - 6x = 16

  • x² - 6x + 9 = 16 + 9

  • x² - 6x + 9 = 25

 

Figure 03: How to Complete the Square in 3 Easy Steps.

 

Step #3: Factor and solve.

Finally, we are ready for the third and final step where we just need to factor and solve.

Notice that the left side of the equation of x² - 6x + 9 = 25 is a trinomial that is factorable as follows:

  • x² - 6x + 9 = (x-3)(x-3)

  • x² - 6x + 9 = (x-3)²

In this example, the factors of x² - 6x + 9 are (x-3)(x-3), which we will express as (x-3)² since it will allow us to solve the problem as follows:

  • x² - 6x + 9 = 25

  • (x-3)² = 25

  • √[(x-3)²] = √[25]

  • x -3 = ± 5

In the third step above, we took the square root of both sides of the equation to remove the exponent and we are left with x -3 = ± 5, which means that

  • x - 3 = 5

  • x - 3 = -5

We can now find the solutions to this first example by solving both equations as follows:

  • x - 3 = 5 → x = 8

  • x - 3 = -5 → x = -2

All three steps for how to do completing the square are shown in Figure 03 above.

Now, we can conclude that the original quadratic equation x² - 6x -16 = 0 has two solutions:

Final Answer: x = 8 and x = -2

This means that the graph of the equation x² - 6x -16 = 0 will be a parabola that crosses the x-axis at both (-2,0) and (8,0) as shown in Figure 04 below.

 

Figure 04: How to solve by completing the square: graph explanation

 

How to Complete the Square: Example #2

Solve: x² +12x +32 = 0

We can solve this next example using our 3-step method, just as we did in the previous example, as follows:

Step #1: Rearrange the quadratic equation so that all of the constants are on one side of the equals sign.

Notice for our given quadratic equation, x² +12x +32 = 0, that a=1, b=12, and c=32.

Since our constant c is on the left side of the equation, we simply have to move it to the right side using inverse operations to complete Step #1.

  • x² +12x + 32 = 0

  • x² +12x + 32 (-32) = 0 (-32)

  • x² + 12x = -32

After completing the first step, we now have:

  • x² + 12x = -32

Step #2: Add (b/2)² to both sides of the equal sign.

Next, we have to add (b/2)² to both sides of our new equation.

In this example, b=12, so we can find the value of (b/2)² as follows:

  • (b/2)²

  • (12/2)²

  • (6)²

  • =36

Since (b/2)² = 36, we can complete Step #2 by adding 36 to both sides of the equation as follows:

  • x² + 12x = -32

  • x² + 12x +36 = -32 +36

  • x² + 12x +36 = 4

 

Figure 05: How to complete the square to find the solutions to a quadratic equation.

 

Step #3: Factor and solve.

For the final step, we just have to factor and solve for any potential values of x.

Just like example #1, we can finish completing the square by factoring the trinomial on the left side of the equation and then solving.

In this case, the trinomial on the left side of the equation can be factored as follows:

  • x² + 12x +36 = (x+6)(x+6)

  • x² + 12x +36 = (x+6)²

❗Note that whenever you solve a problem using the complete the square method, you will always end up with two identical factors when you complete Step #3.

Now that we know that the factors of x² + 12x +36 are equal to (x+6)², we can solve for x as follows:

  • x² + 12x +36 = 4

  • (x+6)² = 4

  • √[(x+6)²] = √[4]

  • x + 6 = ± 2

In this case, the original quadratic function x² +12x +32 = 0 will have two solutions:

  • x + 6 = 2

  • x + 6 = -2

We can determine these two solutions by solving each equation as follows:

  • x + 6 = 2 → x = -4

  • x + 6 = -2 → x = -8

The entire 3-step method for completing the square for Example #2 is shown in Figure 05 above.

Final Answer: x = -4 and x = -8

Figure 06 below shows the graph of the parabola represented by x² +12x +32, with x-intercepts at -4 and -8.

 

Figure 06: Solving a quadratic by completing the square helps you to find the x-intercepts of the parabola that represents the equation.

 

How to Complete the Square: Example #3

Solve: x² +2x -7 = 0

Are you starting to get the hang of how to complete the square? Let’s gain some more experience with this next example.

Step #1: Rearrange the quadratic equation so that all of the constants are on one side of the equals sign.

For this problem, we know that a=1, b=2, and c=-7.

For our first step, let’s rearrange the equation so that all of the constants are on the right side:

  • x² +2x -7 = 0

  • x² +2x -7 (+7) = 0 (+7)

  • x² + 2x = 7

Now we have a new equivalent function:

  • x² + 2x = 7

Step #2: Add (b/2)² to both sides of the equal sign.

Now we need to add (b/2)² to both sides of the equation. Since b=2 in this example, (b/2)² is equal to:

  • (b/2)²

  • (2/2)²

  • (1)²

  • =1

Since (b/2)² = 1, we can complete the second step by adding 1 to each side of the equation as follows:

  • x² + 2x = 7

  • x² + 2x +1 = 7 +1

  • x² + 2x +1 = 8

 

Figure 07: How to Complete the Square: Solutions will not always be rational numbers.

 

Step #3: Factor and solve.

Now we are ready to factor and solve the equation.

We have a trinomial on the left side of the equation that can be factored as follows:

  • x² + 2x +1 = (x+1)(x+1)

  • x² + 2x +1 = (x+1)²

With these factors in mind, we can solve for x as follows:

  • x² + 2x +1 = 8

  • (x+1)² = 8

  • √[(x+1)²] = √[8]

  • x +1 = ± √[8]

For this third example, the quadratic function x² +2x -7 = 0 will have two solutions:

  • x + 1 = √[8]

  • x + 1 = - √[8]

If we continue onto solving these two equations, we will see that, unlike Examples #1 and #2, we do not end up with a rational answer:

  • x + 1 = √[8] → x = -1 + √8

  • x + 1 = - √[8] → x = -1 - √8

In cases like this, you can often conclude that:

Final Answer: x = -1 + √8 and x = -1 - √8

The solutions above are considered exact answers. However, if you are trying to estimate where the parabola will cross the x-axis on the coordinate plane, you could take the problem a step further by approximating for √8 as follows:

  • √8 ≈ 2.83

  • x = -1 + √8 → x = -1 + 2.83 → x =1.83

  • x = -1 + √8 → x = -1 - 2.83 → x =-3.83

Now we have two approximate solutions for x:

  • x =1.83 and x=-3.83

What does this mean? Just like we saw in Examples #1 and #2, the solutions tell you where the graph of the parabola crosses the x-axis. In this example, the graph crosses the x-axis at approximately 1.83 and -3.83, as shown in Figure 08 below.

 

Figure 08:  How to complete the square to determine the solutions to a quadratic equation.

 

Conclusion: How to Complete the Square

When learning how to solve quadratic equations of the form ax² + bx +c=0, understanding how to complete the square to find the values where x=0 is an important and useful algebra skill that you can use to solve a variety of problems.

Whenever you have an equation in ax² + bx +c=0 form, you can solve it by following these 3-simple steps to completing the square:

  • Step #1: Rearrange the quadratic equation so that all of the constants are on one side of the equals sign.

  • Step #2: Add (b/2)² to both sides of the equal sign.

  • Step #3: Factor and solve.

Note that the above 3-step method for completing the square can be used to find the solutions of any quadratic equation of the form ax² + bx +c=0. These solutions represent the x-values where the parabola that represents the equation crosses the x-axis.

Keep Learning:

How to Find the Vertex of a Parabola in 3 Easy Steps

Learn how to find the coordinates of the vertex point of any parabola with this free step-by-step guide.

Comment

How to Find Horizontal Asymptotes in 3 Easy Steps

Comment

How to Find Horizontal Asymptotes in 3 Easy Steps

How to Find Horizontal Asymptotes in 3 Easy Steps

Step-by-Step Guide: How to Find the Horizontal Asymptote of a Function

 

Step-by-Step Guide: How to Find the Horizontal Asymptotes of Functions.

 

During your study of algebra, you will eventually learn how to analyze and understand the behavior functions when they are represented graphically on the coordinate plane. The graph of a function gives you a visual portrayal of how the function behaves—including the location of any potential horizontal asymptotes.

This free step-by-step guide on How to Find Horizontal Asymptotes of a Function will demonstrate and explain everything you need to know about horizontal asymptotes and how to find the horizontal asymptote of any function (assuming that the function does indeed have a horizontal asymptote).

The following sections will be covered in this guide. While we recommend that you work through each section in order, you can use the quick-links below to jump to a particular section":

Let’s start off by learning more about horizontal asymptotes and what they look like.

 

Figure 01: The horizontal asymptote of a function tells you the behavior of a function as it approaches the edges of a graph.

 

What is a Horizontal Asymptote?

Before you learn how to find horizontal asymptotes, it is important for you to understand some key foundational concepts.

In algebra, a function is an equation of the form y=f(x) that represents the relationship between two sets. A relation can be defined as a function when there is only one output value for each input value (i.e. the x-values do not repeat). Functions can be visually represented on a graph (i.e. a coordinate plane).

A horizontal asymptote of a function is a horizontal line (↔) that tells you the behavior of a function as it approaches the edges of a graph. We can also say that horizontal asymptotes allow us to identify the “end behavior” of a function.

It is also important to note that horizontal asymptotes occur when functions are rational expressions, meaning that the function is a quotient of two polynomials (i.e. the function is a fraction where both the numerator and the denominator are polynomials.

For example, consider the following function:

  • y = (3x²)/x³

 

Figure 02: The graph of the function y = (3x²)/x³

 

Our function, y = (3x²)/x³, is the quotient of two polynomials (i.e. it is a rational expression) and its corresponding graph is shown in Figure 02 above.

Since our function is a fraction, we know that we can not have zero in the denominator (otherwise the function would be undefined at this point). So, the graph of the function, as you can see in Figure 02, does something interesting at zero.

In this example, we have a horizontal asymptote at y=0.

Notice how the graph of the function y = (3x²)/x³ gets closer and closer to the line y=0, without ever touching it, as it approaches the ends of the graph (horizontally), as shown in Figure 03 below.

 

Figure 03: The function has a horizontal asymptote at y=0.

 

If we take a look at a few points on the graph of y = (3x²)/x³ and the corresponding table, as shown in Figure 04 below, we can see that as the graph moves to the left of the coordinate plane, the y-values get closer and closer to zero. And, we can also see that as the graph moves to the right of the coordinate plane, the y-values get closer and closer to zero.

This type of observation is what we call determining the “end behavior” and it helps us to understand why the graph has a horizontal asymptote at y=0.

 

Figure 04: How to Find a Horizontal Asymptote of a Function

 

Now that you understand what a horizontal asymptote is and what it looks like, you are ready to work through a few step-by-step examples of how to find a horizontal asymptote.

Before moving forward, here are a few quick key points you should be familiar with:

  • Not all functions that are rational expressions have a horizontal asymptote.

  • It is possible for a function to have 0, 1, or 2 asymptotes (i.e. a function can have a maximum of 2 asymptotes).

  • When horizontal asymptotes are shown on a graph, they are typically drawn using a dashed line, which is what you will see in this guide.

  • The horizontal asymptote of a function is not a part of the function, and it is not a requirement to include the horizontal asymptote of a function when you graph it on the coordinate plane.

  • A horizontal asymptote can be thought of as an imaginary dashed line on the coordinate plane that helps you to visual a “gap” in a graph.

 

Figure 05: A horizontal asymptote is an imaginary line that is not a part of the graph of a function.

 

How to Find Horizontal Asymptotes Example #1

Now you are ready to learn how to find a horizontal asymptote using the following three steps:

  • Step One: Determine lim x→∞ f(x). In other words, find the limit for the function as x approaches positive ∞.

  • Step Two: Determine lim x→-∞ f(x). In other words, find the limit for the function as x approaches negative ∞.

  • Step Three: If one of or both of the limits determined above is a real number, k, then the equation of the horizontal asymptote is y=k for each unique value of k (a function can have 0, 1, or 2 horizontal asymptotes).

Now, let’s go ahead and apply these three steps to our first practice problem.

Example #1: Find the horizontal asymptote of the function f(x)=4x/(x+4)

For this first example, we can start by taking a look at the graph in Figure 05 above. By looking at the graph, we can see that the function f(x)=4x/(x+4) has one horizontal asymptote at y=4.

Let’s now apply our three steps to see if confirm the at the function has a horizontal asymptote at y=4.

Step One: Determine lim x→∞ f(x). In other words, find the limit for the function as x approaches positive ∞.

  • lim x→∞ f(x) = lim x→∞ 4x/(x+4)

  • = 4 lim x→∞ [1/(1+(4/x))]

  • = 4 (lim x→∞ (1)) / (lim x→∞ (1+(4/x))

  • = 4 ( (1)/(1))

  • =4

After completing the first step, we can see that, as the function has a horizontal asymptote at y=4 as the function approaches positive ∞ on the graph.

Next, let’s confirm that the function has the same behavior as it approaches negative ∞.

Step Two: Determine lim x→-∞ f(x). In other words, find the limit for the function as x approaches negative ∞.

  • lim x→-∞ f(x) = lim x→∞ 4x/(x+4)

  • = 4 lim x→-∞ [1/(1+(4/x))]

  • = 4 (lim x→-∞ (1)) / (lim x→∞ (1+(4/x))

  • = 4 ( (1)/(1))

  • =4

Completing the second step gives us the same result as the first step (i.e. there is a horizontal asymptote at y=4).

Step Three: If one of or both of the limits determined above is a real number, k, then the equation of the horizontal asymptote is y=k for each unique value of k (a function can have 0, 1, or 2 horizontal asymptotes).

Finally, based on our results from steps one and two, we can conclude that the function has one horizontal asymptote at y=4, as shown on the graph in Figure 06 below.

Final Answer: The function has one horizontal asymptote at y=4.

 

Figure 06: How to find a horizontal asymptote using limits.

 

How to Find Horizontal Asymptotes Example #2

Find the horizontal asymptote of the function f(x)=3ˣ+5

For this next example, we want to see if the exponential function f(x)=3ˣ+5 has any horizontal asymptotes.

We can solve this problem the same as we did the first example by using our three steps as follows:

Step One: Determine lim x→∞ f(x). In other words, find the limit for the function as x approaches positive ∞.

  • lim x→∞ f(x) = lim x→∞ 3ˣ+5

  • =lim x→∞ (3ˣ) + lim x→∞ (5)

  • lim x→∞ (3ˣ) = ∞

  • lim x→∞ (5) = 5

  • = ∞ + 5 = ∞

Notice that our result for the first step is that, as the function approaches positive ∞, the limit is ∞. And, since ∞ is not a real number, we can not yet determine whether or not this function will have any horizontal asymptotes. But we can not be completely sure until we complete the second step.

Step Two: Determine lim x→-∞ f(x. In other words, find the limit for the function as x approaches negative ∞.

  • lim x→-∞ f(x) = lim x→-∞ 3ˣ+5

  • =lim x→-∞ (3ˣ) + lim x→-∞ (5)

  • lim x→-∞ (3ˣ) = 0

  • lim x→-∞ (5) = 5

  • = 0 + 5 = 5

Our result from step number two results in a real number, so we can conclude that the function does have a horizontal asymptote at y=5.

Step Three: If one of or both of the limits determined above is a real number, k, then the equation of the horizontal asymptote is y=k for each unique value of k (a function can have 0, 1, or 2 horizontal asymptotes).

Again, even though Step One did not result in a real number limit, Step Two did, so we can conclude that:

Final Answer: The function has one horizontal asymptote at y=5.

We can confirm the location of a horizontal asymptote at y=5 for the exponential function f(x)=3ˣ+5 by looking at the completed graph in Figure 07 below.

 

Figure 07: How to find horizontal asymptotes given a function explained.

 

How to Find Horizontal Asymptotes Example #3

Find the horizontal asymptote of the function f(x)=(3x^2+x)/(x+2)

For this third and final example, we have to see if the rational function f(x)=(3x^2+x)/(x+2) has one, two, or zero horizontal asymptotes.

We can determine whether or not the function has any horizontal asymptotes by following our three steps as follows:

Step One: Determine lim x→∞ f(x). In other words, find the limit for the function as x approaches positive ∞.

  • lim x→∞ f(x) = lim x→∞ (3x^2+x)/(x+2)

  • =lim x→∞ (3x+1)/(1+(2/x))

  • = (lim x→∞ (3x+1)) / (lim x→∞(1+(2/x)))

  • lim x→∞ (3x+1) = ∞

  • lim x→∞(1+(2/x)) = 1

  • = ∞ / 1 = ∞

Since our result is not a real number, Step One does not help us to determine the possible existence of a horizontal asymptote.

Step Two: Determine lim x→-∞ f(x. In other words, find the limit for the function as x approaches negative ∞.

  • lim x→-∞ f(x) = lim x→-∞ (3x^2+x)/(x+2)

  • =lim x→-∞ (3x+1)/(1+(2/x))

  • = (lim x→-∞ (3x+1)) / (lim x→-∞(1+(2/x)))

  • lim x→-∞ (3x+1) = -∞

  • lim x→-∞(1+(2/x)) = 1

  • = -∞ / 1 = -∞

Again, our result is not a real number so we can not determine the location of a horizontal asymptote.

Step Three: If one of or both of the limits determined above is a real number, k, then the equation of the horizontal asymptote is y=k for each unique value of k (a function can have 0, 1, or 2 horizontal asymptotes).

Since neither Step One nor Step Two resulted in a real number value for k, we can conclude that the function does not have any horizontal asymptotes.

Final Answer: The function does not have any horizontal asymptotes.

The graph of the function f(x)=(3x^2+x)/(x+2) is shown in Figure 08 below. Do you notice how there is no horizontal asymptote?

 

Figure 08: How to Find Horizontal Asymptotes: Not all functions will have a horizontal asymptote.

 

Conclusion: How to Find Horizontal Asymptotes

A horizontal asymptote of a function is an imaginary horizontal line (↔) that helps you to identify the “end behavior” of the function as it approaches the edges of a graph.

Not every function has a horizontal asymptote. Functions can have 0, 1, or 2 horizontal asymptotes.

If a function does have any horizontal asymptotes, they will be displayed as a dashed line. A horizontal asymptote is an imaginary line that is not a part of the function, and it is not a requirement to include the horizontal asymptote of a function when you graph it on the coordinate plane.

You can determine whether or not any function has horizontal asymptotes by following these three simple steps:

  • Step One: Determine lim x→∞ f(x). In other words, find the limit for the function as x approaches positive ∞.

  • Step Two: Determine lim x→-∞ f(x). In other words, find the limit for the function as x approaches negative ∞.

  • Step Three: If one of or both of the limits determined above is a real number, k, then the equation of the horizontal asymptote is y=k for each unique value of k (a function can have 0, 1, or 2 horizontal asymptotes).

Keep Learning:

How to Find the Vertex of a Parabola in 3 Easy Steps

Learn how to find the coordinates of the vertex point of any parabola with this free step-by-step guide.

Comment

How to Find the Circumference of a Circle in 3 Easy Steps

How to Find the Circumference of a Circle in 3 Easy Steps

How to Find the Circumference of a Circle

Step-by-Step Guide: What is the circumference of a circle? How to find the circumference of a circle using the formula for circumference of a circle?

 

Free Step-by-Step Guide: How to find the circumference of a circle explained.

 

Understanding how to find the circumference of a circle is an important math skill that every student must learn.

In order to learn how to find the circumference of a circle, you need to be familiar with the concept of circumference and how to use the formula for circumference of a circle to solve problems where you are tasked with finding the length of a circle’s circumference.

This free Step-by-Step Guide on How to Find the Circumference of a Circle will teach you how to use the circle formula, C=πd, to find circumference of a circle. The guide is organized by the following sections/subtopics:

While we recommend that you work through in section in order, you can use the links above to jump to any section of interest.

Are you ready to get started? Let’s begin with a review of some important properties of circles that you will need to be familiar with in order to learn how to find the circumference of a circle.

 

Figure 01: Do you know the key properties of circles?

 

What is the Circumference of a Circle?

Before we get into what the circumference of a circle actually means, there are some key circle-related vocabulary terms that you should be familiar with:

  • A circle’s diameter is any line that passes through the center point of the circle and touches two points on the edge of the circle.

  • A circle’s radius is any line segment that runs from the center point and touches the edge of the circle.

  • A radius of a circle, r, will always be equal to half the length of its diameter, d. In other words, r=2d.

  • Conversely, the diameter of a circle, d, will always be equal to twice the length of its radius, r. In other words, d=2r.

These key properties of circles are illustrated in Figure 01 above for your reference. Make sure that you understand them well before moving on.

What is the circumference of a circle?

The circumference of a circle is the length of its outer boundary. The circumference of a circle is sometimes referred to as a perimeter of a circle and it is always measured in units such as inches, centimeters, yards, etc.

In real-world terms, you could find the circumference of a circle by taking the outer boundary of a circle and flattening it out into a straight line and then measuring the length of that straight line. Whatever the length is would be the circumference of the circle.

For example, if you have a section of rope that was 4 feet long and you curled it into a perfect circle, the circle will also have a circumference of 4 feet, as shown in Figure 02 below.

 

Figure 02: What is the circumference of a circle?

 

The biggest takeaway here is that the circumference of a circle is the total length of the outer region of the circle. You could imagine taking a circle, cutting it somewhere, and then bending it so it forms a straight line. You could then find the circumference by measuring that straight line.

The diagram in Figure 03 below further illustrates the concept of circumference in mathematical terms.

Now that you understand what the circumference of a circle represents, let’s move onto the next section, where will we learn the circumference of a circle formula.

 

Figure 03: What is the circumference of a circle?

 

Circumference of a Circle Formula: C=πd

You can find the circumference of any circle simply by using the circumference of a circle formula: C=πd (where d is the length of the diameter of the circle).

In other words, circumference equals pi times diameter.

Whenever you are using the circumference of a circle formula, you have the option of using pi (π) or an approximation of pi (π≈3.14). If you have a calculator that has a π button, we highly recommend using it instead of approximating pi as 3.14, since it will give you more accurate answers. However, both options are acceptable in most cases.

Before continuing onto the next section, be sure to remember that the d in the circumference formula represents the length of the circle’s diameter. You can use the diagram in Figure 04 below as a reference for remembering that the circumference of a circle formula is C=πd.

 

Figure 04: The circumference of a circle formula is C=πd (circumference equals pi times diameter).

 

For example, let’s say that we wanted to find the circumference of a circle with a diameter of 10 cm. Knowing that d=10 in this example, we could solve this problem by using the circumference of a circle formula as follows:

  • C=πd and d=10

  • C=π(10) or C=10π

  • C=31.41592654…

  • C=31.4 cm

So, we can conclude that the circle has an approximate circumference of 31.4 centimeters. We figured this out by substituting d with 10 in the formula to get C=π(10) or C=10π (this both mean the same thing—the product of 10 and π) and using our calculator to get C=31.41592654…, which we rounded to the nearest tenth decimal place to get C=31.4 cm.

Note that we will be expressing circumference to the nearest tenth of decimal place for all of the examples in this guide.

The step-by-step process for finding the circumference of a circle with a diameter of 10cm is shown in Figure 05 below.

 

Figure 05: How to use circumference of a circle formula.

 

Now that you know how to use the circumference formula, you are ready to learn how to find the circumference of a circle by working through a several examples.

How to Find Circumference of a Circle with Diameter

In the previous section, we learned how to find the circumference of a circle with diameter of 10cm. The step-by-step process for solving thing problem is illustrated in Figure 05 above.

As long as you know that the circle circumference formula is C=πd, you can solve any problem where you have to find the circumference of a circle with diameter given. To do this, simply substitute d with the numerical value of the length of the diameter and then multiply it by π to determine the length of the circle’s circumference.

This method is exactly how we will solve our first practice problem. Let’s go ahead and get started.

Example #1: Find the Circumference of a Circle with Diameter 17 mm

For this first example, we have to find the circumference of a circle with diameter of 17 mm.

We can solve this problem by using the circumference of a circle formula, C=πd, by inputting d=17 into the formula and solving as follows:

  • C=πd

  • C=π(17) pr C=17π

  • C=53.40707511…

  • C=54.4 mm

Final Answer: The circle has a circumference of 54.4 mm.

Finished! As long as you know the length of a circle’s diameter, you can input it into the circle circumference formula to calculate its circumference.

The step-by-step process for solving Example #1 are shown in Figure 06 below. Be sure that you are comfortable with this process before moving onto the next example.

 

Figure 06: How to Find the Circumference of a Circle Step-by-Step.

 

Example #2: Find the Circumference of a Circle with Diameter 20.6 yd

For this next example, we want to calculate the circumference of a circle with diameter 20.6 yd.

Notice that the value of the diameter, d, in this example is a decimal. However, you can still use the formula, C=πd, to solve this problem and find the circumference of the circle as follows:

  • C=πd

  • C=π(20.6) or C=20.6π

  • C=64.71680866…

  • C=64.7 yd

Final Answer: The circle has a circumference of 64.7 yd.

This process for using the circumference of a circle formula to find the circumference of a circle with a diameter of 20.6 yd is illustrated in Figure 06 below.

 

Figure 06: How to find the circumference of a circle when the diameter is given.

 

Now, let’s work through one more example of how to find circumference of a circle with diameter in a real-world context.

Example #3: Find the Circumference of a Circle with Diameter 60 meters

For this third example, we want to find the circumference of a paved sidewalk that surrounds a circular pond with a diameter that is 60 meters long.

Even though this is a real-world scenario, we can still use the circumference formula to find the answer as follows:

  • C=πd

  • C=π(60) or C=60π

  • C=188.4955592…

  • C=188.5 m

Final Answer: The paved sidewalk has a circumference of 188.5 meters.

The diagram in Figure 07 illustrates this real-world scenario and how we used our formula to figure out the circumference of the path that surrounds the circular pond.

 

Figure 07: How to find the circumference of a circle in a real-world scenario.

 

How to Find Circumference of a Circle with Radius

You probably have learned that finding the circumference of a circle when you are given the length of its diameter is a pretty straightforward process, but what happens when only know the length of the circle’s radius and not the length of its diameter?

As long as you understand the relationship between a circle’s radius and its diameter, you can easily use a given radius to figure out the length of the diameter. And this skill is extremely useful because it will allow you to use the circumference of a circle formula, C=πd, to solve circle problems where only the radius is given.

Recall from our vocabulary review at the start of this guide that a radius of a circle is any line segment that starts at the center and ends on the edge of the circle and that the radius of a circle is equal to half the length of the circle’s diameter.

  • r = d/2

Conversely, we can say that the diameter of a circle is equal to twice the length of its radius:

  • d=2r

So, if you know the length of the radius of a circle, you can use it to find the length of the diameter, d, by multiplying it by 2.

For example, if you were given a circle with a radius of 5 feet (r=5). You could take the radius and double it to find the value of the diameter, which, in this case, would be 10 ft.

  • r=5

  • d=2r

  • d=2(5)

  • d=10

The diagram in Figure 08 below illustrates this relationship between the radius and the diameter of a circle.

The key takeaway is that the diameter of a circle is equal to twice the length of its radius.

Now, let’s go ahead and apply our understanding of this relationship to another practice problem.

 

Figure 08: The diameter of a circle is equal to twice the length of its radius (d=2r).

 

Example #4: Find the Circumference of a Circle with Radius of 7 inches

In this example, we have to find the circumference of a circle with a radius of 7 inches (r=7).

Our goal is to solve this problem the same way that we solved the three previous examples where we calculated circumference using the formula C=πd.

However, the difference between Example #4 and the previous three is that, in this case, we are given the radius of the circle, r, and not the diameter.

But we can use the given radius, r=7, to find the length of the diameter, d, because we know that the diameter of a circle is equal to twice the length of its radius:

  • d=2r

  • d=2(7)

  • d=14

Therefore, if the circle has a radius of 7 inches, then it also has a diameter of 14 inches (because 7x2=14).

Now that we know the value of d (d=14 in this case), we can substitute it into the circumference of a circle formula and solve as follows:

  • C=πd

  • C=π(14) or C=14π

  • C=43.98229715

  • C=44.0 in

Final Answer: The circle has a circumference of 44 inches.

The entire step-by-step process for solving this fourth and final example are illustrated in Figure 09 below. If you are still confused about how to find the circumference of a circle, we recommend that you go back and work through the practice problems again.

 

Figure 09: How to find the circumference of a circle with a given radius.

 

How to Find the Circumference of a Circle: Conclusion

The circumference of a circle, also known as its perimeter, is the length of its outer boundary.

Understanding how to find the circumference of a circle is a foundational math skill that has many practical applications both inside and outside of the math classroom.

Whenever you have to find the circumference of a circle, you can use the formula C=πd, where d represents the lengths of the circle’s diameter, to find an answer.

If you are given the length of the circle’s diameter, you can substitute it for d in the formula and solve. However, if you only know the circle’s radius, you will have to multiply it by two (d=2r) to find the length of its diameter, d, before you can use the formula.

However, as long as you know the circumference of a circle formula and the relationship between the radius and diameter of a circle, you can easily calculate the circumference of a circle in just a few simple steps.

Keep Learning: