Quadratic Formula Examples Tutorial
Step-by-Step Guide: Examples of How to Find the Roots of a Quadratic Function using the Quadratic Formula
Are you ready to work through a few quadratic formula examples to gain some more practice and experience with solving quadratic equations using the quadratic formula?
In math, the quadratic formula, x= (-b ± [√(b² - 4ac)]) / 2a is an incredibly important and useful formula that you can use to find the solutions (also known as roots) or any quadratic equation of the form ax² + bx + c = 0 (where a ≠ 0), whether it is easy to factor or not!
If you know how to use the quadratic formula, then you can solve a variety of algebra problems involving quadratic equations, and learning how to use it correctly is something that you can easily learn with some practice and repetition.
This free Quadratic Formula Examples Step-by-Step Guide includes a short review of the quadratic formula as well as several different practice problems that we will work through and solve using the quadratic formula with a step-by-step explanation. The guide is organize by the following sections, and you can click on any of the hyperlinks below to jump to any particular spot:
Before we dive into any of the quadratic formula examples, let’s start off with a quick review of the quadratic formula and why it is such a useful algebra tool.
Figure 01: The Quadratic Formula
What is the Quadratic Formula?
Before you can learn how to use the quadratic formula, it is important that you understand what a quadratic equation is.
Definition: A quadratic equation is a function of the form ax² + bx + c = 0 (where a does not equal zero). On a graph, a quadratic equation can be represented by a parabola. The x-values where the parabola crosses the x-axis is called the solutions, or roots, of the quadratic equation.
For example, consider the following quadratic equation:
x² + 5x + 6 = 0
Notice that this equation is in ax² + bx + c = 0 form, where…
a=1
b=5
c=6
If we want to find the solutions, or roots, of this quadratic equation, we have a few options.
First, we could factor this quadratic equation by looking for two values that add to 5 and also multiply to 6, which, in this case, would be 2 and 3. So we could say that…
x² + 5x + 6 = 0 → (x+2)(x+3) = 0
We could then solve for each factor as follows:
x + 2 = 0 → x = -2
x + 3 = 0 → x = -3
Now we can conclude that the solutions of this quadratic are x=-2 or x=-3.
Figure 02: What are the solutions (or roots) of a quadratic equation?
Another option for finding the solutions to a quadratic equation is to look at its graph. The solutions, or roots, will be the x-values where the graph crosses the x—axis. Note that quadratic equations can have two roots, one root, or even no real roots (as you will see later in this guide).
As for the equation x² + 5x + 6 = 0, the corresponding graph in Figure 02 above confirms that the equation has solutions at x=-2 and x=-3.
But what do we do when a quadratic equation is very difficult to factor or when we do not have access to a clear graph? Well, this is where the quadratic formula comes into play.
Definition: Any quadratic equation of the form ax² + bx + c = 0 (where a ≠ 0), can be solved using the quadratic formula, which states that…
x= (-b ± [√(b² - 4ac)]) / 2a
Why is the quadratic formula so useful? Because, as the definition states, it can be used to find the solutions to any quadratic equation. While the quadratic equation that we just looked at, x² + 5x + 6 = 0, was pretty easy to work with and solve, it is considered extremely simple. As you move farther along your algebra journey, you will come across more and more complex quadratic equations that can be very difficult to factor or even graph.
However, if you know how to use the quadratic formula, you can successfully solve any quadratic equation. With this in mind, let’s go ahead and work through some quadratic formula examples so you can gain some practice.
And we will start by using it to solve x² + 5x + 6 = 0, because we already know that the solutions are x=-2 and x=-3. If the quadratic formula works, then it should yield us that same result. Once we work through this first simple example, we will move onto more complex examples of how to use the quadratic formula to solve quadratic equations.
Figure 03: To use the quadratic formula, start by identifying the values of a, b, and c.
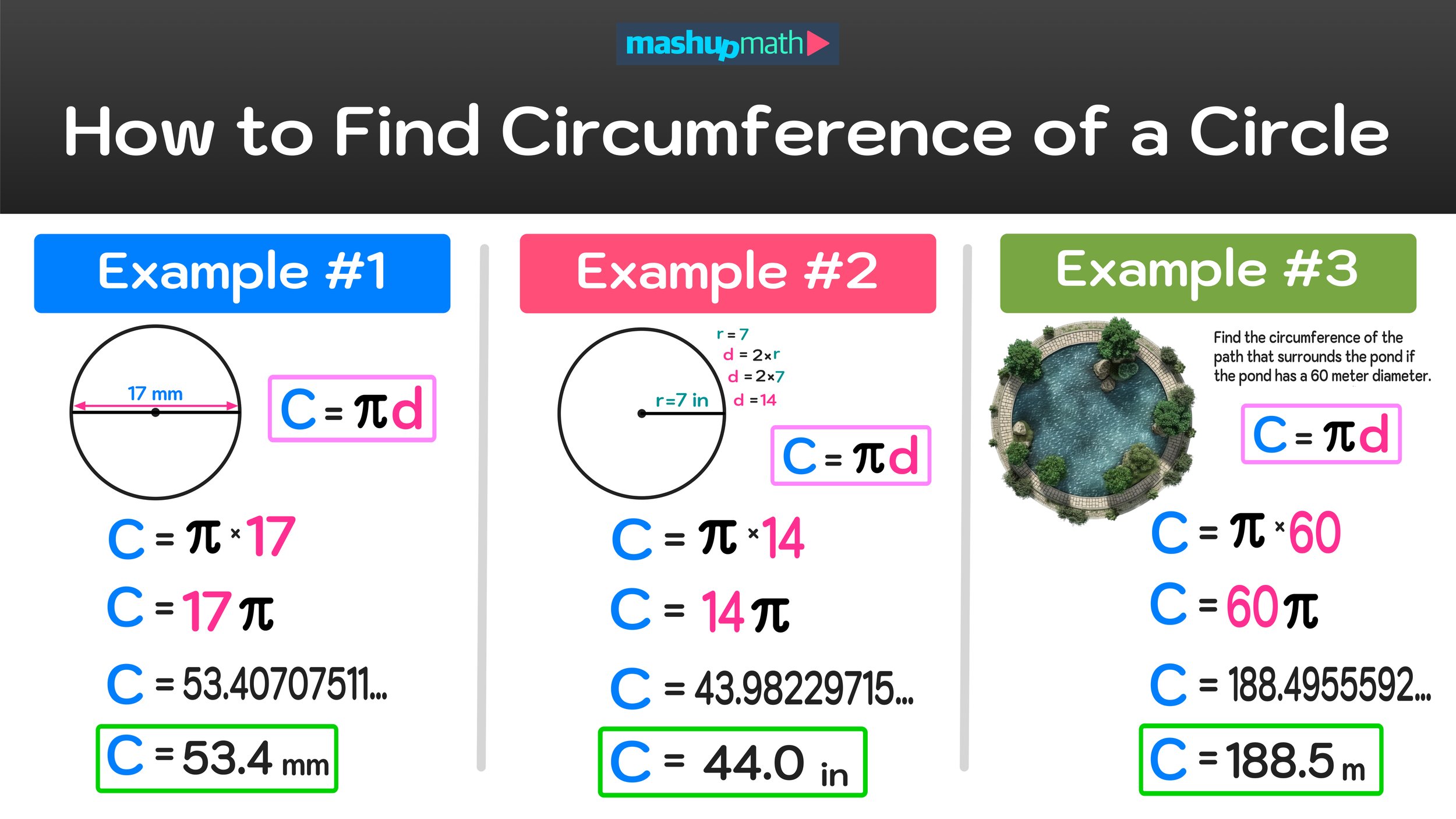
Quadratic Formula Examples
We will begin by using the quadratic formula to solve the equation shown in Figure 02 above: x² + 5x + 6 = 0
Example #1: Solve x² + 5x + 6 = 0
First, notice that our equation is in ax² + bx + c = 0 form where:
a=1
b=5
c=6
Identifying the values of a, b, and c will always be the first step (provided that the equation is already in ax² + bx + c = 0 form).
Now that we know the values of a, b, and c, we can plug them into the quadratic equation as follows:
x= (-b ± [√(b² - 4ac)]) / 2a
x= -(5) ± [√(5² - 4(1)(6))]) / 2(1)
x= -5 ± [√(25 - 24)] / 2
x= -5 ± [√(1)] / 2
x= (-5 ± 1) / 2
Now we are left with x= (-5 ± 1) / 2. Note that the ± mean “plus or minus” meaning that we have to split this result into two separate equations:
Plus: x = (-5 + 1) / 2
Minus: x = (-5 - 1) / 2
By solving these two separate equations, we can find the solutions to the quadratic function x² + 5x + 6 = 0.
x = (-5 + 1) / 2 = -4/2 = -2 → x=-2
x = (-5 - 1) / 2 = -6/2 = -3 → x=-3
After solving both equations, we are left with x=-2 and x=-3, which we already knew were the solutions to x² + 5x + 6 = 0. So, we have confirmed that the quadratic formula can be used to find the solutions to any quadratic equation of the form ax² + bx + c = 0.
Final Answer: x=-2 and x=-3
The steps to solving the quadratic formula example is illustrated in Figure 04 below.
Figure 04: Quadratic Formula Examples Step-by-Step
Example #2: Solve 2x² + 2x -12 = 0
For our next quadratic formula example, we will again start by identifying the values of a, b, and c as follows:
a=2
b=2
c=-12
Make sure that you correctly identify the sign (positive or negative) as well, since this is necessary to using to quadratic formula correctly.
Next, we can substitute these values for a, b, and c into the quadratic formula as follows:
x= (-b ± [√(b² - 4ac)]) / 2a
x= -(2) ± [√(2² - 4(2)(-12))]) / 2(2)
x= -2 ± [√(4 - -96)] / 4
x= -2 ± [√(100)] / 4
x= (-2 ± 10) / 4
Our result is x= (-2 ± 10) / 4. From here, we can rewrite e the result as two separate equations by “spitting” the ± sign as follows:
Plus: x= (-2 + 10) / 4
Minus:x= (-2 - 10) / 4
Now we can solve each individual equation to find the values of x that will be the solutions of this quadratic equation.
x= (-2 + 10) / 4 = 8/4 = 2 → x=2
x = (-2 - 10) / 4 = -12/4 = 3 → x=3
We are left with two values for x: x=2 and x=-3, and we can conclude that the quadratic equation 2x² + 2x -12 = 0 has the following solutions:
Final Answer: x=2 and x=-3
Figure 05 shows the step-by-step process for solving this quadratic formula example.
Figure 05: Quadratic Formula Examples #2 Solved
Example #3: Solve 2x² -5x + 3 = 0
For the next of our quadratic formula examples calls for us to use the quadratic formula to find the solutions to a quadratic function where:
a=2
b=-5
c=3
The process of substituting a, b, and c into quadratic formula will be exactly the same as the last two quadratic formula examples.
x= (-b ± [√(b² - 4ac)]) / 2a
x= -(-5) ± [√(-5² - 4(2)(3))]) / 2(2)
x= 5 ± [√(25 - 24)] / 4
x= 5 ± [√(1)] / 4
x= (5 ± 1) / 4
Are you starting to get the hang of it? Now that we have simplified our equation, we are left with x= (5 ± 1) / 4. And, just like the last two examples, we can go ahead and split this result into two separate equations as follows:
Plus: x= (5 + 1) / 4
Minus: x= (5 - 1) / 4
Finally, we just have to solve each equation to get our final answer (i.e. the values of the solutions).
x= (5+1) / 4 = 6/4 = 3/2 → x=3/2
x= (5-1) / 4 = 4/4 = 1 → x=1
Notice that the result of the first equation ended up as a fraction (3/2). This is totally fine! It just means that the parabola will cross the x-axis in the middle of a box (rather than hitting directly at an integer coordinate).
Final Answer: x=3/2 and x=1
All of the steps for solving this example are shown in Figure 06 below.
Figure 06: Sometimes a quadratic formula will give you a solution that is a fraction.
Example #4: Solve 3x² + 2 = 7x
The fourth and final of our quadratic formula examples looks a bit different. The given equation 3x² + 2 = 7x is not in ax² + bx + c = 0 form.
Whenever this is the case, we will have to see if we can use algebra to rearrange the equation so to make into ax² + bx + c = 0 form. We can do that by using inverse operations to move the 7x to the left-side of the equation as follows:
3x² + 2 = 7x
3x² + 2 (-7x) = 7x (-7x)
3x² + 2 -7x = 0
Notice that result, 3x² + 2 -7x = 0, still isn’t in ax² + bx + c = 0 form. However, the commutative property allows us to rearrange the terms as follows:
3x² + 2 -7x = → 3x² -7x +2
Now we have an equivalent equation, 3x² -7x +2=0, that is in ax² + bx + c = 0 form, where:
a=3
b=-7
c=2
Sometimes you will be given equations that have to be rearranged in order to use the quadratic formula. If you can not rearrange an equation so that it can be expressed in ax² + bx + c = 0 form, then you can not solve it using the quadratic formula.
This example, however, can now be solved using the quadratic formula as follows:
x= (-b ± [√(b² - 4ac)]) / 2a
x= -(-7) ± [√(-7² - 4(3)(2))]) / 2(3)
x= 7 ± [√(49 - 24)] / 6
x= 7 ± [√(25)] / 6
x= (7 ± 5) / 6
Now we are left with a much easier equation to work with: x= (7 ± 5) / 6. Let’s go ahead and split it into two separate equations to solve it:
Plus: x= (7 + 5) / 6
Minus: x= (7 - 5) / 6
We can solve for x in each equation as follows:
x= (7+5) / 6 = 12/6 = 2 → x=2
x= (7-5) / 6 = 2/6 = 1/3 → x=1/3
Final Answer: x=2 and x=1/3
That’s all that there is to it! You can review of the steps to solving this quadratic formula example by looking at the illustration in Figure 07 below.
Figure 07: Quadratic Formula Examples: Rearranging an equation to put it into ax² + bx + c = 0 form.
Do you need more practice with using the Quadratic Formula?
Check out our free library of Quadratic Formula Worksheets (with answer keys)