How to Add Fractions with Different Denominators
Math Skills: How to Add Fractions with Unlike Denominators in 3 Easy Steps
Ready to learn how to add fractions with unlike denominators?
When it comes to working with fractions and performing operations on them, you will typically first learn how to add fractions. Once you master how to add fractions with the same denominator, it’s time to advance to a more challenging task—learning how to add fractions with different denominators (or unlike denominators).
While adding fractions with a common denominator is relatively simple and straightforward, things get a bit trickier when you are tasked with adding fractions that do not have the same denominator. However, learning how to add fractions with unlike denominators is a skill that every math student can learn by becoming familiar with a few simple steps and by working on a sufficient amount of practice problems (which is exactly what we will be doing in this guide).
This free How to Add Fractions with Different Denominators guide is your step-by-step tutorial to learning how to add fractions with uncommon denominators together. In this guide, we will use an easy 3-step method for adding fractions that you can use to solve any problem where you have to find the sum of two fractions that do not share the same denominator.
You can follow this guide in order (recommended if you are new to adding fractions) or by using the quick-links below to jump to a specific section or example.
Are you ready to get started?
Before we start working on any practice problems, let’s do a quick review of some key vocabulary as well as how to add fractions with unlike denominators.
Review: Adding Fractions with the Same Denominator
First, let’s make sure that we understand the difference between the numerator and the denominator of a fraction.
Definition: The top number of any fraction is called the numerator. For example, the fraction 5/7 has a numerator of 5.
Definition: The bottom number of any fraction is called the denominator. For example, the fraction 5/7 has a denominator of 7.
In this guide, we will be making reference to numerators and denominators often, so make sure that you understand what these terms mean before moving on.
Figure 01: In any fraction, the numerator is the top number and the denominator is the bottom number.
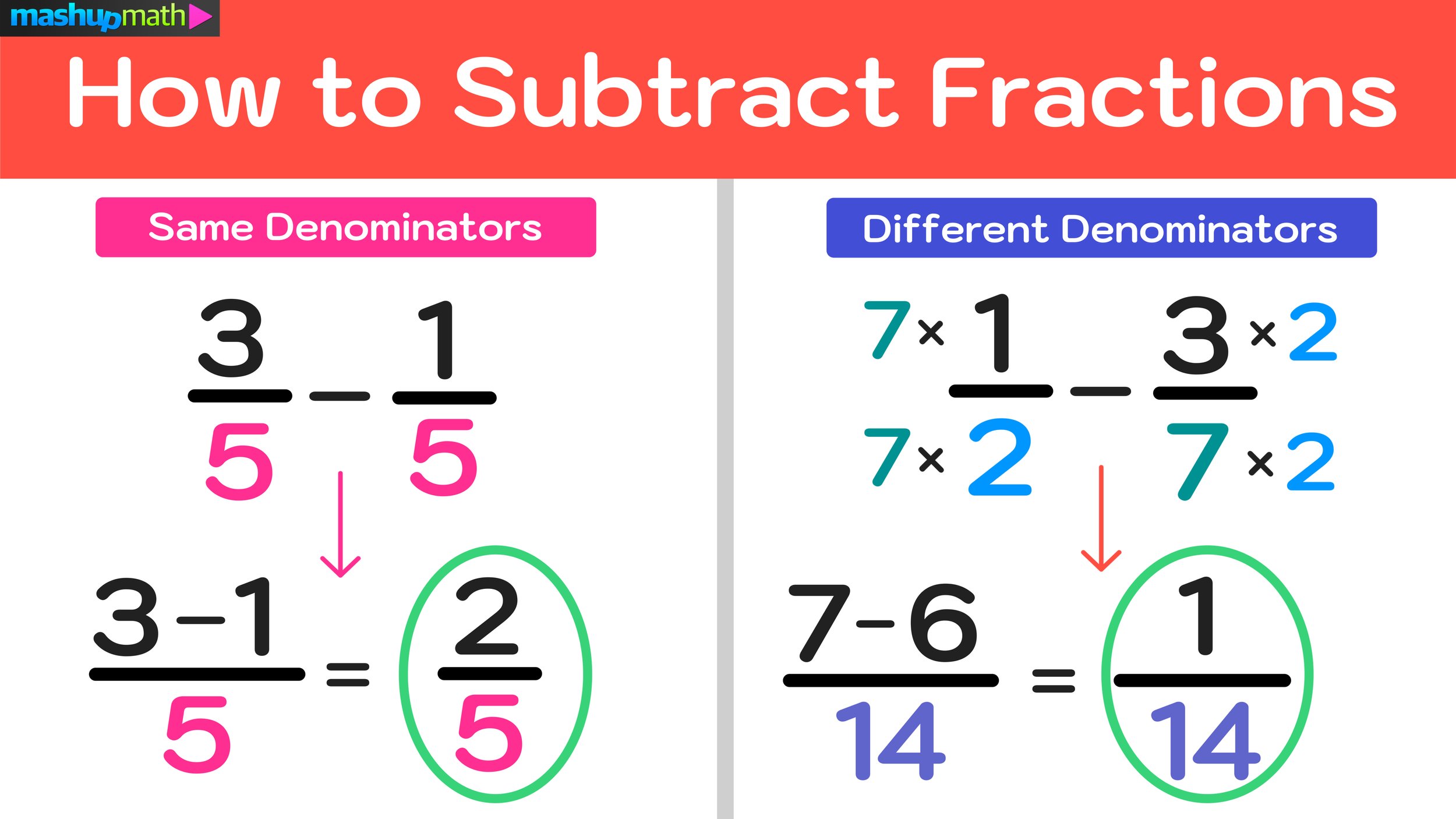
When it comes to adding fractions, the process is relatively simple when the denominators are the same.
For example, what if you wanted to solve the following problem:
1/4 + 2/4 = ?
Notice that the fractions 1/4 and 2/4 have the same denominator (i.e. they both have a denominator of 4).
In cases like this, when both fractions have the same denominator, you can simply add the numerators together and keep the denominator the same as follows:
1/4 + 2/4 = (1+2)/4 = 3/4
And, since 3/4 can not be simplified any further, we can say that:
Final Answer: 1/4 + 2/4 = 3/4
The process for solving this problem is illustrated in Figure 02 below. If you need a more in-depth review of how to add fractions with the same denominator, we recommend checking out our free guide to adding fractions before moving on.
Key Takeaway: When adding fractions with the same denominator, you can simply add the numerators together and keep the same denominator.
Figure 02: When adding fractions with the same denominator, you can simply add the numerators together and keep the same denominator.
Now that we have recapped how to add fractions when the denominators are the same, we are ready to learn to how to add fractions with unlike denominators.
How to Add Fractions with Unlike Denominators in 3-Easy Steps
Now, let’s revisit the practice problem from the previous section where we had to add two fractions with the same denominator:
1/4 + 2/4 = ?
We already solved this problem and determined that the answer is 3/4. Now, let’s consider another problem where the denominators are different:
1/4 + 1/2 = ?
In this new problem, the first fraction has a denominator of 4 and the second fraction has a denominator of 2 (i.e. the fractions have unlike denominators).
However, notice that the second fraction in the first problem, 2/4, and the second fraction in the second problem, 1/2, are equivalent since they both represent one-half.
This means that both problems mean the same thing (i.e. find the sum of one-quarter and one-half) and that they will both have the same answer: 3/4.
With this in mind, let’s learn a 3-step method for adding fractions with unlike denominators and apply it to the problem 1/4 + 1/2 = ? to see if it gives us a result of 3/4.
Figure 03: Two different ways to write the expression “one-quarter plus one-half.” One has like denominators and the other has different denominators.
How to Add Fractions with Unlike Denominators:
Step One: Get a common denominator by multiplying each fraction by the other’s fraction’s denominator (top and bottom).
Step Two: Add the numerators together and keep the denominator.
Step Three: Simplify the result if possible.
That’s all there is to it! Now, let’s go ahead and apply these three steps to 1/4 + 1/2 = ?
Step One: Get a common denominator by multiplying each fraction by the other’s fraction’s denominator (top and bottom).
For this initial step, you have to find a common denominator—a value that the denominators of both fractions divide evenly into.
The easiest way to find a common denominator is to multiply the denominator of the first fraction by the second fraction and then multiply denominator of the second fraction by the first fraction as follows:
1/4 + 1/2 = (2x1)/(2x4) + (4x1)/(4x2) = 2/8 + 4/8
Doing this gives us a new equivalent expression that now has a common denominator (both fractions have a denominator of 8). The actions taken to complete this first step are illustrated in Figure 04 below.
Figure 04: How to Add Fractions with Unlike Denominators: You can find a common denominator by multiplying each fraction by the other fraction’s denominator.
Step Two: Add the numerators together and keep the denominator.
Now we have a new expression where both fractions share a common denominator:
1/4 + 1/2 → 2/8 + 4/8
Next, we have to add the numerators together and keep the denominator as follows:
2/8 + 4/8 = (2+4)/8 = 6/8
Step Three: Simplify the result if possible.
Finally, we are left with the fraction 6/8 and we only have to see if the fraction can be simplified. Since 6 and 8 share a greatest common factor of 2, we can divide both 6 and 8 by 2 to get 3/4 (i.e. the fraction 6/8 simplifies to 3/4) and we can conclude that:
Final Answer: 1/4 + 1/2 = 3/4
Figure 05: How to Add Fractions with Different Denominators in 3 Easy Steps.
This answer should make sense sill we already knew that the end result was going to be 3/4. Now that you are familiar with the 3-step method for adding fractions with different denominators, let’s gain some practice applying them to three different practice problems.
How to Add Fractions with Different Denominators Example #1
Example #1: 2/3 + 1/5
For our first example, we have to find the sum of two-thirds (2/3) and one-fifth (1/5). Let’s go ahead and use our 3-step method to add fractions with unlike denominators:
Step One: Get a common denominator by multiplying each fraction by the other’s fraction’s denominator (top and bottom).
Let’s start by finding a common denominator by multiplying the denominator of the first fraction (3) by the second fraction (1/5) and then multiply denominator of the second fraction (5) by the first fraction (2/3) as follows:
2/3 + 1/5 = (5x2)/(5x3) + (3x1)/(3x5) = 10/15 + 3/15
Now we have a new expression that is equivalent to the original, except the fractions now have the same denominator:
2/3 + 1/5 → 10/15 + 3/15
Step Two: Add the numerators together and keep the denominator.
Next, we can perform 10/15 + 3/15 as follows:
10/15 + 3/15 = (10+3)/15 = 13/15
Step Three: Simplify the result if possible.
For the third and final step, we have to see if we can simplify the result (13/15). Since 13 and 15 do not share any common factors other than 1, we can not simplify this fraction any further and we can conclude that:
Final Answer: 2/3 + 1/5 = 13/15
Figure 06 below shows how we determined that 2/3 + 1/5 = 13/15 using our 3-step method.
Figure 06: How to Add Fractions with Unlike Denominators
How to Add Fractions with Unlike Denominators Example #2
Example #2: 2/9 + 3/7
We can go ahead and solve this next example by using our 3-step method just like we did for Example #1:
Step One: Get a common denominator by multiplying each fraction by the other’s fraction’s denominator (top and bottom).
We can find a common denominator by multiplying the first fraction (2/9) by 7 and the second fraction (3/7) by 9 as follows:
2/9 + 3/7 = (7x2)/(7x9) + (9x3)/(9x7) = 14/63 + 27/63
From here, we have a new equivalent expression to what we started with:
2/9 + 3/7 → 14/63 + 27/63
Step Two: Add the numerators together and keep the denominator.
For the second step, we can find the solve of 14/63 + 27/63 as follows:
14/63 + 26/63 = (14+27)/63 = 41/63
Step Three: Simplify the result if possible.
Lastly, we have to determine whether or not the result, 41/63, can be simplified. Since 41 and 63 do not share a greatest common factor other than 1, we know that the fraction can not be reduced and:
Final Answer: 2/9 + 3/7 = 41/63
The entire process for solving Example #2 is displayed in Figure 07 below.
Figure 07: Adding Fractions Explained!
By now, you should be starting to feel a little more comfortable with using our 3-step method for solving problems where you have to add fractions with unlike denominators. Let’s gain some more experience by working through one more example.
How to Add Fractions with Different Denominators Example #3
Example #3: 3/18 + 2/16
We can solve this final example using our 3-step method as follows:
Step One: Get a common denominator by multiplying each fraction by the other’s fraction’s denominator (top and bottom).
We can find a common denominator by multiplying each fraction by the other fraction’s denominator:
3/18 + 2/16 = (16x3)/(16x18) + (18x2)/(18x16) = 48/288 + 36/288
By the end of step one, we are left with a new equivalent expression:
3/18 + 2/16 → 48/288 + 36/288
Step Two: Add the numerators together and keep the denominator.
Continue by solving 48/288 + 36/288:
48/288 + 36/288 = (48+36)/288 = 84/288
Step Three: Simplify the result if possible.
We’re almost finished. For the third and last step, we have to see if 84/288 can be simplified. Since 84 and 288 share a greatest common factor of 12, we can divide both the numerator, 84, and the denominator, 288, by 12 to get an equivalent reduced fraction, 7/24.
Final Answer: 3/18 + 2/16 = 7/24
Our entire step-by-step approach to solving this last example where we had to add fractions with unlike denominators is shown in Figure 08 below.
Figure 08: How to Add Fractions with Different Denominators
Conclusion: How to Add Fractions with Different Denominators in 3 Easy Steps
Understanding how to add fractions is an important math skill that every student must learn. When it comes to adding fractions, there are two common scenarios that you must be familiar with:
Adding Fractions with Like Denominators
Adding Fractions with Unlike Denominators
The focus of this guide is on teaching you how to deal with problems related to the second scenario: how to add fractions with unlike denominators.
To solve problems where you have to add fractions with unlike denominators, we learned to use the following 3-step method for how to add fractions with unlike denominators:
Step One: Get a common denominator by multiplying each fraction by the other’s fraction’s denominator (top and bottom).
Step Two: Add the numerators together and keep the denominator.
Step Three: Simplify the result if possible.
By working through three practice problems, we gained experience with adding fractions with unlike denominators to find correct answers that are in simplified form. Since this method can be used to solve any problem where you have to add fractions with unlike denominators, you can use it solve any math problems resembling the ones covered in this guide!