What is the Vertical Line Test in Math?
Key Question: What is the vertical line test function and how can it be used?
Learning how to identify whether or not a given relation is a function is an extremely important math skill (most notably in pre-algebra and algebra). Luckily, there is a simple and handy tool called the vertical line test that you can always use to see if a relation can be considered a function or not just by looking at its graph.
This free Vertical Line Test step-by-step guide will teach you how to figure out whether or not a relation is or is not a function by looking at its graph and using a simple mathematical tool called the vertical line test.
Before you learn how to use the vertical line test, we will do a quick review of some very important vocabulary and definitions related to functions and relations.
Are you ready to get started?
Vertical Line Test Definitions and Vocabulary
What is a relation?
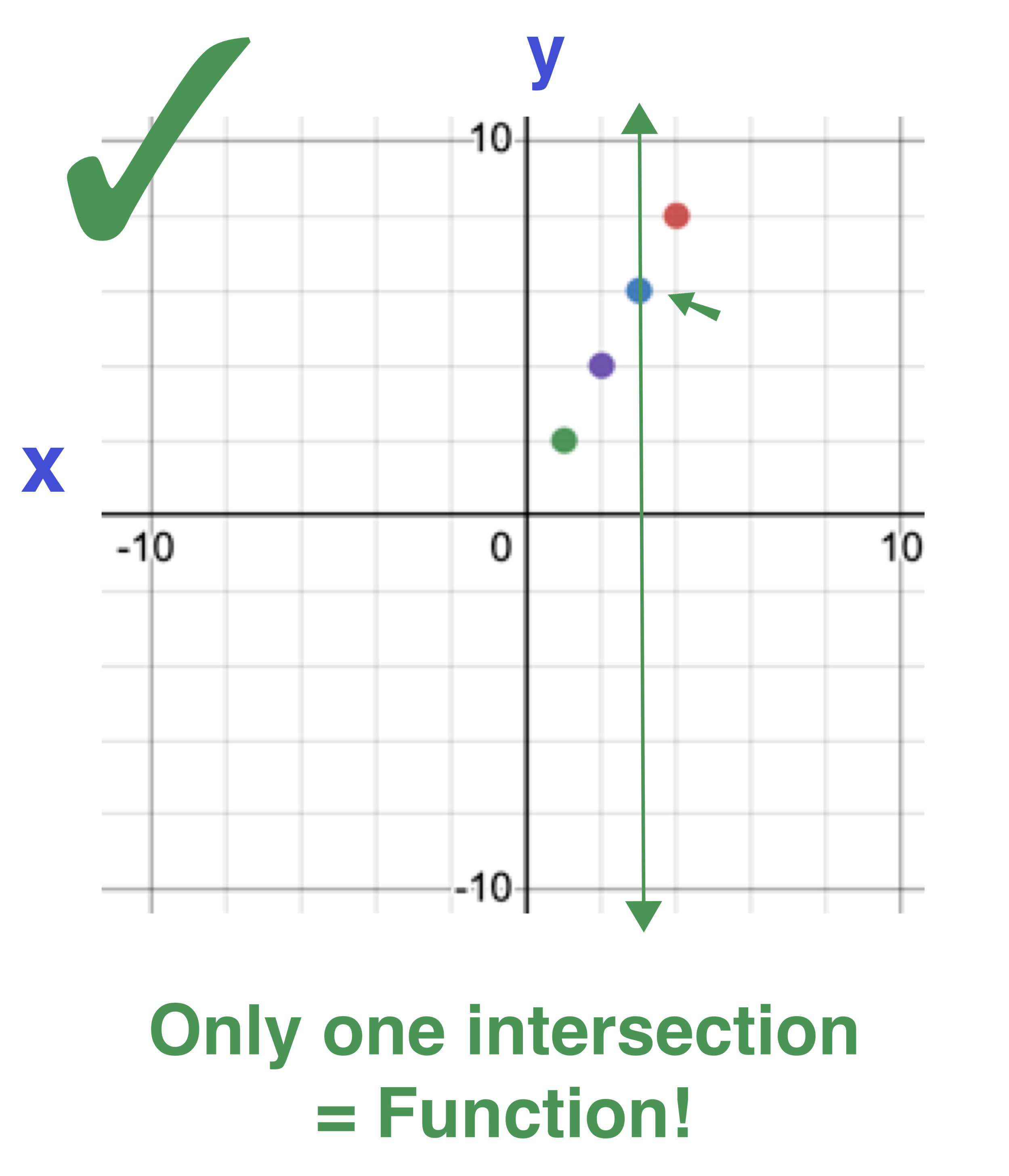
Definition: A relation is how a set of inputs and outputs of a system are related to each other. Mappings and graphs are the most common ways of representing relations. The figures below show a graphic and map representation of the relation between a set of numbers and the square of those numbers.
Figure 01: Relation Mapping
Figure 02: The graph representing the relation in Figure 01.
What is a function?
Definition: A function is a relation between a set of inputs and outputs where, for every input, there is one (and only one) output. In other words, a function is a relation where every input has only one output.
If this is confusing, observe the mappings in Figure 03 and Figure 04 below for more insight.
Figure 03: The relation is a function.
Figure 04: The relation is NOT a function.
The relation mapping in Figure 03 represents a function because every input (or x-value) has only one unique output (or y-value).
The relation mapping in Figure 04 does not represent function because at least one of the inputs (in this case 6) has more than one output. If you look at the mapping, you will notice that 6 has two outputs: 1 and 3. Thus, the relation in Figure 04, by definition, is not function.
Keep this information in mind as we move on and extend your understanding of relations and functions to looking at graphs and learning how to apply the vertical line test.
What is the difference between a relation and a function?
Functions are a subset of relations. Simply put, all functions are relations, but not all relations are functions.
In other words, a relation represents the relationship between an input and an output, while a function—more specifically—is a type of relation where there is only one output for each input.
What is the Vertical Line Test Function?
Now that you understand how to determine whether or not a relation is a function by looking at a mapping, you are ready to learn to make this same determination just by looking at a relation’s graph and using a tool called the vertical line test.
The Vertical Line Test helps you to determine if a given relation is a function. Now, let's find out how the vertical line test works with realistic examples.
Again, for a relation to be a function, the relation must have exactly one output for a given input. Let's revisit the relations shown in Figure 03 and Figure 04, but this time we will represent them graphically:
Figure 05: The graph of the relation in Figure 03, which was, by definition, a function.
Figure 06: The graph of the relation in Figure 04, which was, by definition, not a function.
We already know that the graph in Figure 05 represents a function and that the graph in Figure 06 does not represent a function because we already applied the definition of a function to the corresponding mappings.
But what if we had to make this determination using only the graph without the mappings? This is where the vertical line test comes into play.
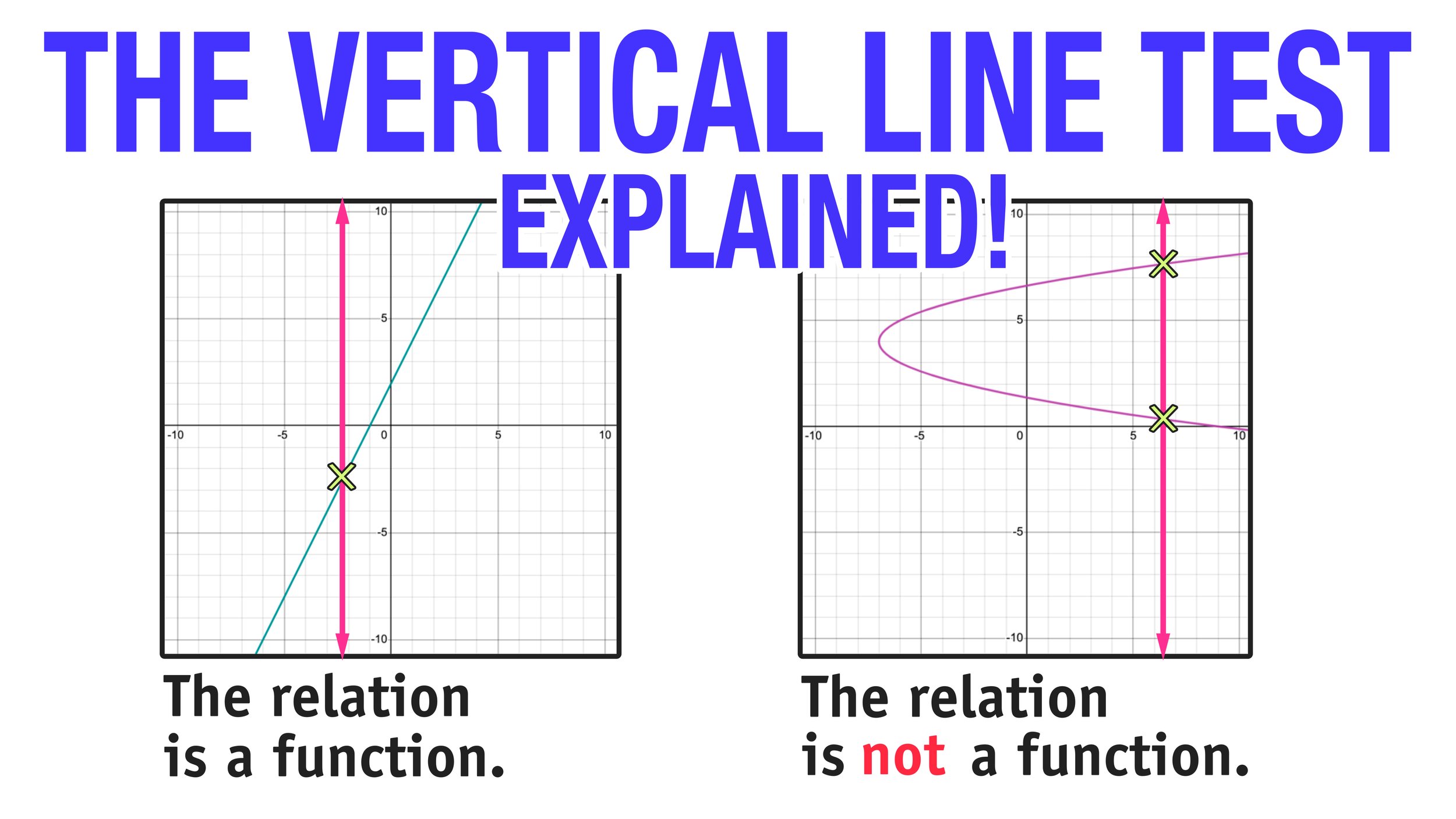
The Vertical Line Test Explained in 3 Easy Steps
The vertical line test is a simple and straightforward tool for determining whether not the graph of a relation represents a function or not.
Applying the vertical line test is as easy as following these 3 easy steps:
Step One: Observe the given graph and draw one or multiple vertical lines through the graph.
Step Two: Note how many times the vertical line(s) that you drew intersected the graph (either coordinate points or a line/curve).
Step Three: Based on the number of intersections, determine whether or not the relation is a function.
If your vertical line intersects the graph only once, then the relation is a function.
If your vertical line intersects the graph more than once at any point, the relation is not a function.
We can apply the vertical line test to the graphs from Figure 05 and Figure 06 below to confirm what we already knew (that one graph represents a function and the other does not).
Figure 07: The vertical line test confirms that the relation is a function because there is only one intersection point.
Figure 08: The vertical line test confirms that the relation is a not function because there are multiple intersection points.
Notice how the vertical line drawn on the graph in Figure 07 only has one intersection point. Furthermore, there are no other areas on the graph where you could draw a vertical line where there would be more than one intersection point. Therefore, the graph represents a function.
Notice how the vertical line drawn on the graph in Figure 08 has multiple intersection points (namely through (6,1) and (6,3)), therefore this graph does not represent a function.
Now that you understand how the vertical line test works, let’s apply it to three more examples…
Vertical Line Test Examples
Directions: Use the vertical line test to determine whether or not the graph of each relation is a function.
Example A: Is the relation a function?
We can determine whether or not this graph represents a function by drawing one (or multiple vertical lines) through the graph to see if there is any point where the line intersects the graph more than once (if it does, then the relation is not a function).
The vertical line test shows…
Here we can clearly see that the relation fails the vertical line test and that the graph does not represent a function because there are multiple intersection points.
Final Answer: The relation is not a function because it fails the vertical line test.
Example B: Is the relation a function?
Again, you can use the vertical line test to determine whether or not the graph above represents a function.
Here we can clearly see that the relation passes the vertical line test and that the graph represents a function because there is only one intersection point.
Final Answer: The relation is a function because it passes the vertical line test.
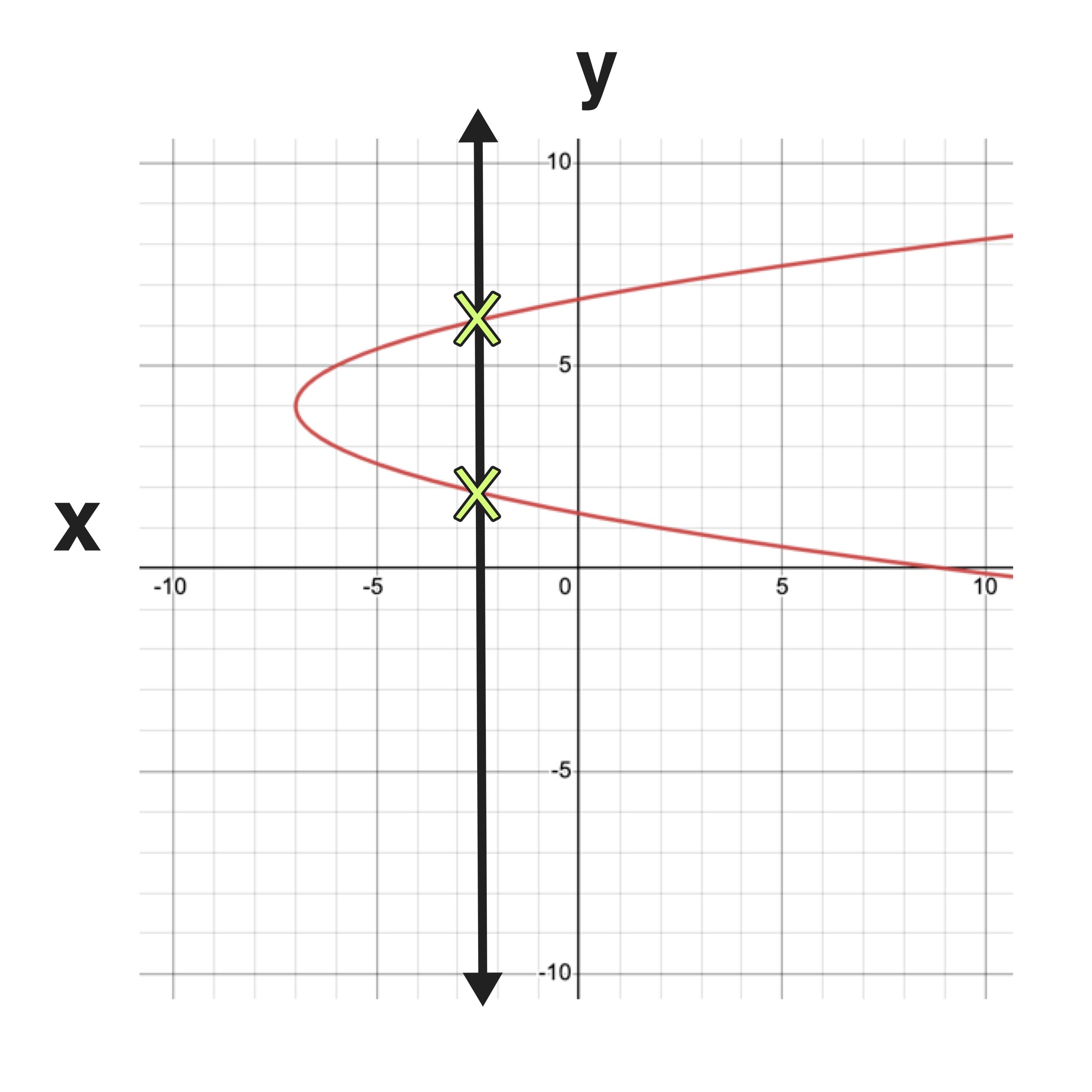
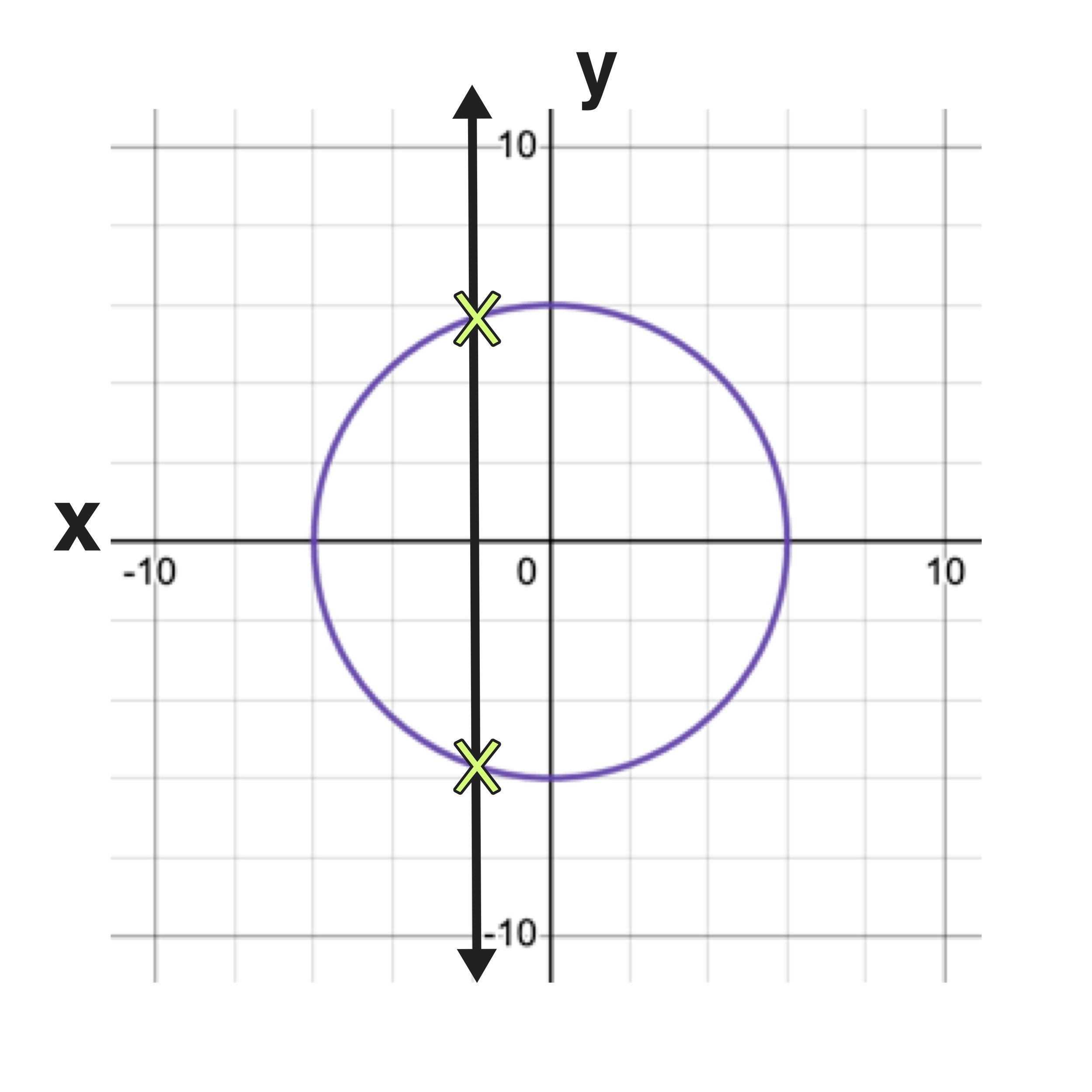
Example C: Is the relation a function?
Are you starting to get the hang of it? Go ahead and apply the vertical line test to see if the graph of the circle represents a function.
Here we can clearly see that the relation fails the vertical line test and that the graph does not represent a function.
Final Answer: The relation is not a function because it fails the vertical line test.
(This will always be the case with circles)
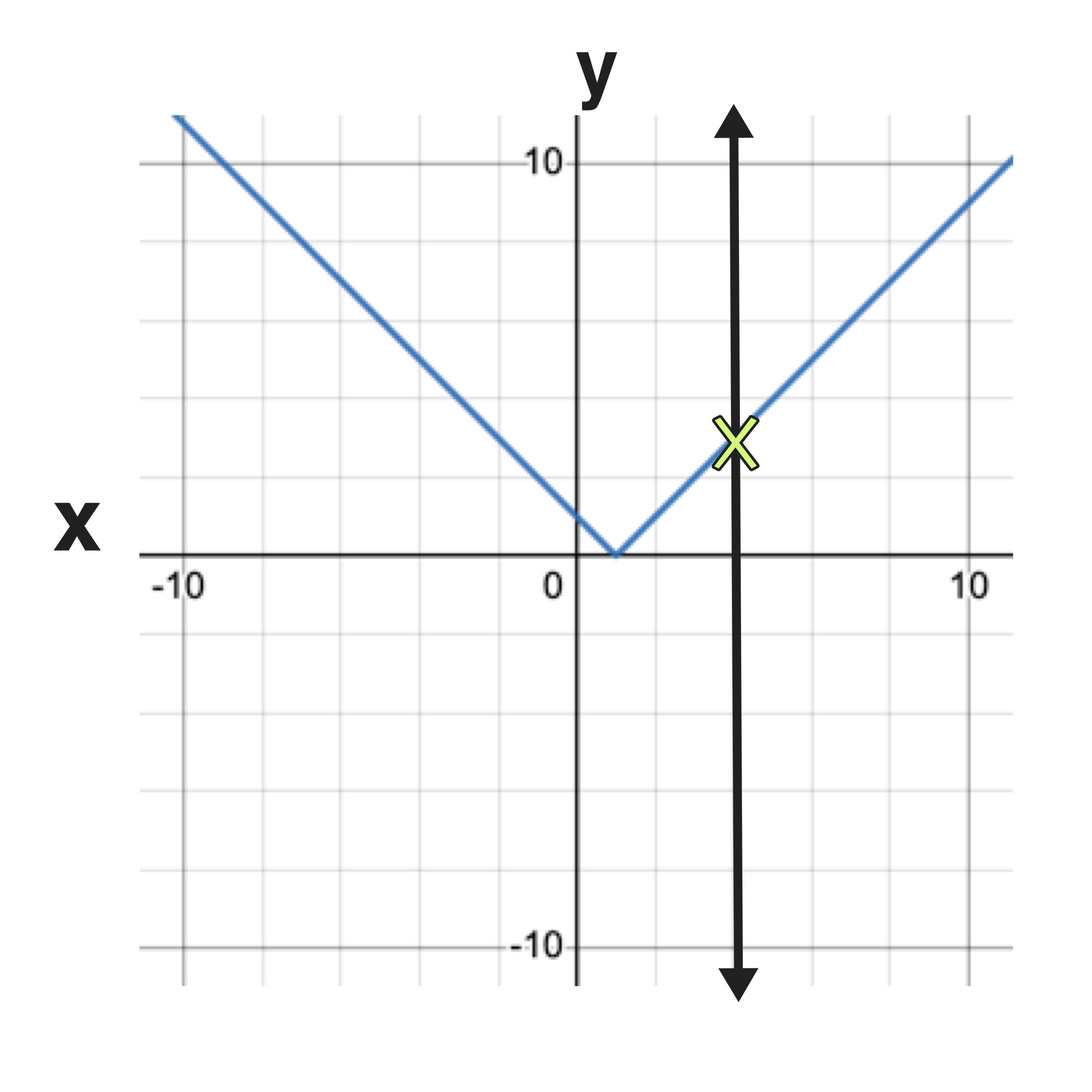
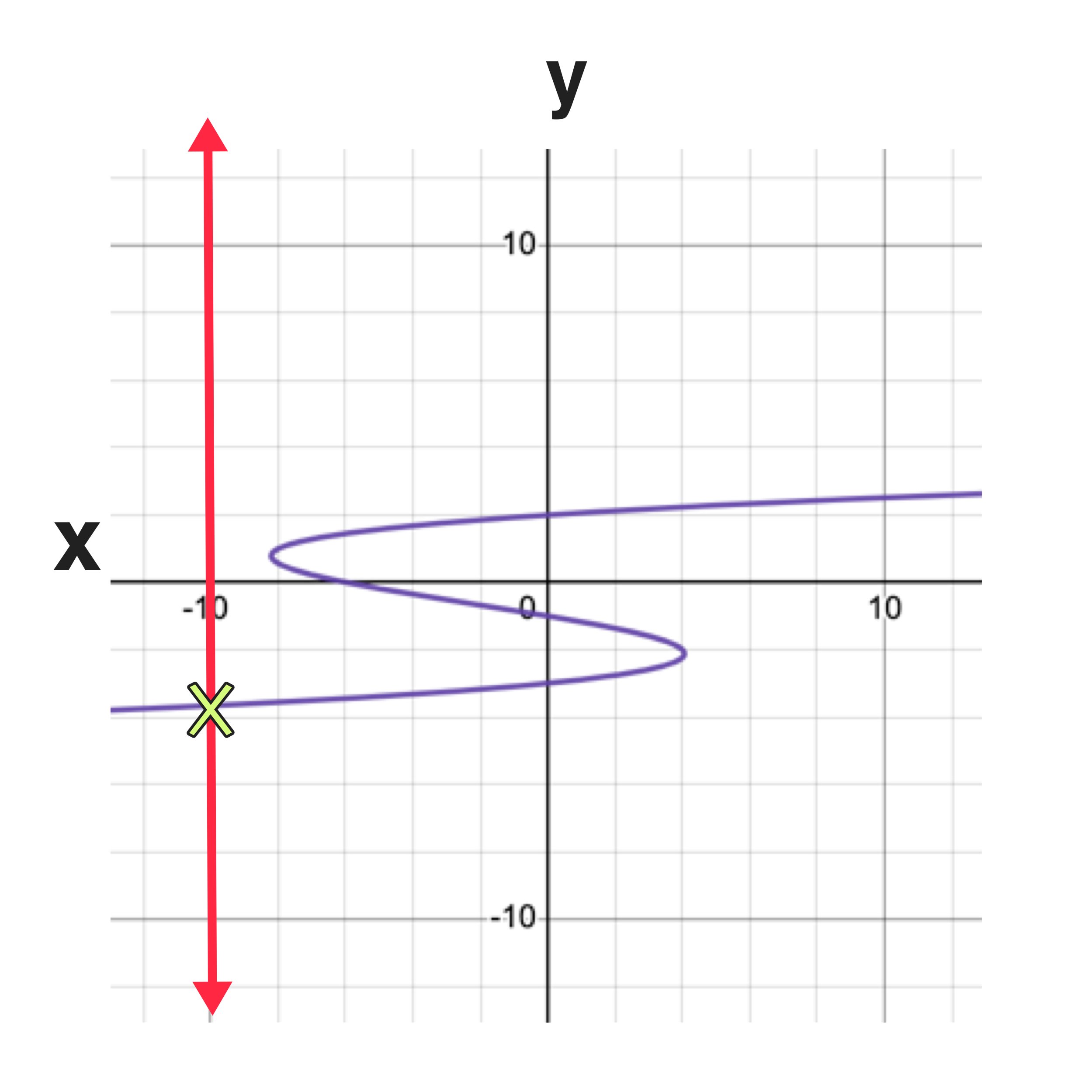
Example D: Is the relation a function?
Remember that the graph of a relation has to pass the vertical line test everywhere in order to confirm that the relation is a function.
For example, if you drew your vertical line at x=-10 as in Figure 09 below, you might incorrectly conclude that the graph passes the vertical line test (since there is only one intersection point).
But, if you draw multiple vertical lines, such as the one through x=2 in Figure 10 below, you will see that this graph actually fails the vertical line test.
Figure 09: Does the vertical line test pass everywhere?
Figure 10: If the vertical line test fails anywhere on the graph, then the relation is not a function.
Final Answer: The relation is not a function because it fails the vertical line test.
Conclusion/Recap:
The vertical line test is a simple, yet effective tool that can be used to determine whether or not the graph of any given relation represents a function (a specific type of relation where for every input there is one and only one output). To make this determination, simply draw a vertical line through the graph and see how many times the vertical line intersects with the graph of the function. If the vertical line only intersects with the graph one time at any given point, then the graph represents a function. However, if the vertical line intersects with the graph at any point more than once, then the graph does not represent a function.
Recap:
Search Tags: vertical line test, vertical line test function, vertical line test examples, the vertical line test, vertical line test definition math, vertical line test to determine function, vertical line test practice
Keep Learning: