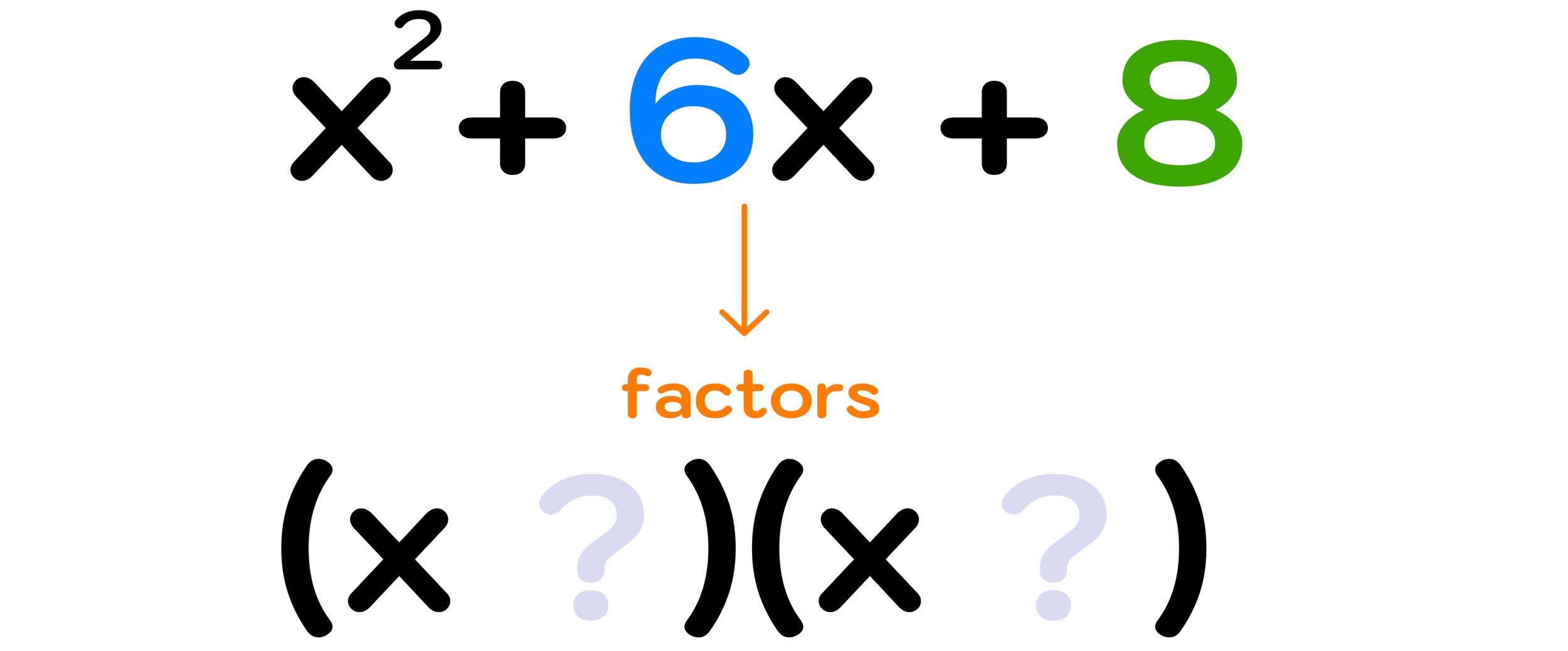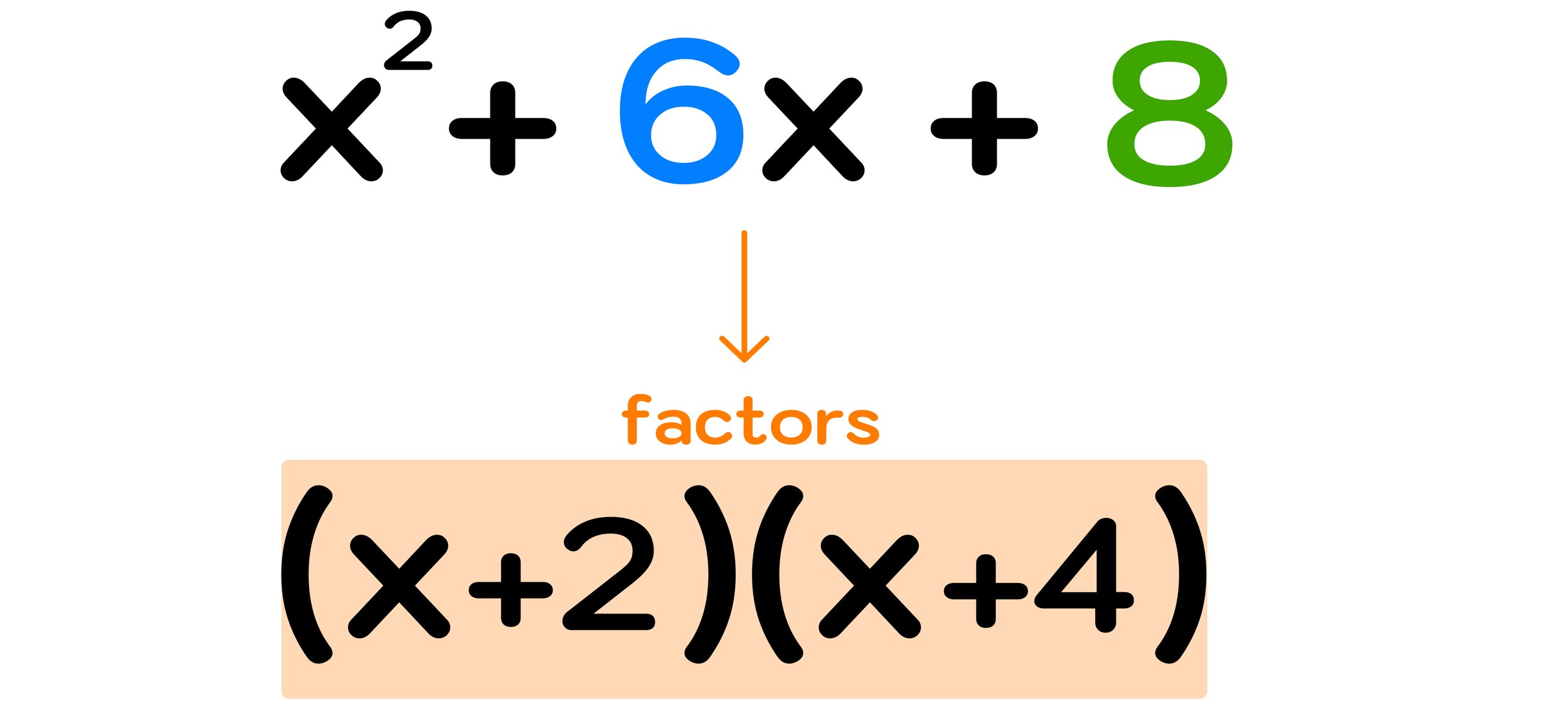How to Factor Quadratic Equations Explained

Step-by-Step Guide: How to Factor a Quadratic Equation, How to Solve Quadratic Equations by Factoring

In algebra, a quadratic equation is an equation of the form ax² + bx + c = 0 where a can not equal zero.

The word quad is Latin for four or fourth, which is why a quadratic equation has four terms (ax², bx, c, and 0). Being able to solve quadratic equations by factoring is an incredibly important algebra skill that every student will need to learn in order to be successful in Algebra I, Algebra II, and beyond. Learning how to factor a quadratic equation comes down to being able to recognize a quadratic equation, being able to factor it, and then finally being able to solve for x and check your answer for mistakes.

This free Step-by-Step Guide on How to Factor Quadratic Equations will cover the following topics:

What is a Quadratic Equation?
What are the Solutions of a Quadratic Equation?
How to Factor Quadratic Equations when a=1
How to Factor Quadratic Equations when a≠1?

Note that this guide is a follow-up to our free step-by-step guide How to How to Factor Polynomials, which reviews how to factor polynomials with 2 terms, 3 terms, and 4 terms. While we will review general factoring in this guide, we will be more focused on how to factor a quadratic equation.

However, before we learn how to factor quadratic equations and how to solve quadratic equations by factoring, let’s quickly review some important vocabulary terms related to quadratics and quadratic equations.

What is a Trinomial Expression?

While the focus of this guide is on teaching you how to factor quadratic equations and how to solve quadratic equations by factoring, it is important that you first understand how the difference between a trinomial expression and a quadratic equation.

In algebra, a trinomial expression is a polynomial with 3 terms of the form ax² + bx + c. Note that, since it is an expression, a trinomial does not include an equal sign.

ax² + bx + c

What is a Quadratic Equation?

In algebra, a quadratic equation is a trinomial of the form ax² + bx + c that is equal to zero. So, we can say that a quadratic equation is of the form:

ax² + bx + c = 0

Figure 01 above illustrates this key difference between trinomial expressions and quadratic equations, which is namely that a quadratic equation is an equation and includes a fourth term (=0).

Why are we concerned with quadratic equations being equal to zero? You may already know that, when graphed, quadratic equations can be represented on the coordinate plane as a parabola (a U-shaped curved). When we solve quadratic equations by factoring, we are actually figuring out where the parabola crosses zero on the x-axis, as shown in Figure 02 below.

Consider the example quadratic in Figure 02 above:

x² +6x + 8 = 0

Notice that, for this quadratic equation, a=1, b=6, and c=8. When it comes time to learn how to factor a quadratic equation later on, it will be important that you are able to identify the values of a, b, and c for any given quadratic equation.

Now, here are two key pieces of information about the solutions to quadratic equations:

The solution(s) to any quadratic equation are the points where the graph of the quadratic crosses the x-axis on a graph.
Quadratic equations typically have two solutions, but they can also have one solution or zero solutions.
You do not have to graph quadratic functions to solve them. You can solve quadratic equations by factoring.

Now that you understand what the solutions of a quadratic represent graphically, you are ready to learn how to factor equations and solve them algebraically.

Are you ready to get started?

How to Factor Quadratic Equations: Intro

Let’s start by factoring the example quadratic equation from Figure 02 above: x² +6x + 8 = 0

Example #1: Factor and Solve x² +6x + 8 = 0

From our graph, we already know that this quadratic equation will have two solutions: x=-4 and x=-2 (note that this can also be written as x={-4,-2}). So, let’s use factoring to find these answers algebraically.

To factor a quadratic equation, we can split it up into two parts:

The left side of the equal sign
The right side of the equal sign

On the left side of the equal sign, we must have a trinomial of the form ax² + bx + c to deal with and, on the right side, we must have a zero. If the quadratic equation in question is not in this form, we will have to use algebra to rearrange it. However, this first example is good to go so we don’t have to move any of the terms around. This first step is shown in Figure 03 below:

From here, the next step is to factor the trinomial on the left side of the equal sign:

x² +6x + 8

Note that, for this introductory example, the value of a (the leading coefficient) is 1. When this is the case, you can factor the trinomial on the left-side of the equation as follows:

Step One: Identify the values of b and c.

In this example, the values of b and c are: b=6 & c=8

Step Two: Find two numbers that both ADD to b and MULTIPLY to c.

Once you have identified the values of b and c (6 and 8 respectively in this example), you can use trial-and-error to find two numbers that both add to the b term (6) and multiply to the c term (8). Another way to say this is: find two numbers with a sum of 6 and a product of 8.

For example, let’s say that you chose the numbers 5 and 1. In this case, 5+1=6, but 5x1≠ 8, so these two numbers would not work.

5 + 1 =6 (the value of b) ✓

5 x 1 ≠ 8 (the value of c) ✘

However, if you chose the numbers 2 and 4:

2 + 4 =6 (the value of b) ✓
2 x 4 = 8 (the value of c) ✓

Since the sum of 2 and 4 is 6 and the product of 2 and 4 is 8, you can found out that the factors of the trinomial x² + 6x + 8 are (x+2) and (x+4)

Step Three: Use your numbers from step two to write out the factors

In this case, you can conclude that the factors of x² + 6x + 8 are (x+2) and (x+4).

How do you know if you result is correct? You can check your answer by performing double distribution as follows:

(x+2)(x+4) = x² + 2x + 4x + 7 = x² + 6x + 8

If the result is the same trinomial that you started with, then you know that your factors are correct.

Now we have a new equation:

(x+4)(x+2)=0

This is not our final answer. To solve this quadratic by factoring, we have to take each factor, set it equal to zero, and solve to find our solutions as follows:

x+4 = 0 → x = -4
x+2 = 0 → x = -2

Final Answer: The quadratic equation x² + 6x + 8=0 has a solution of x={-4,-2}.

This solution should make sense since we already knew from the graphing the parabola that this particular quadratic would equal zero at x=-4 and x=-2.

Now that Example #1 is complete, you know exactly how to factor quadratic equations and how to solve quadratic equations by factoring. However, the way that you factor will vary by problem as not all trinomials are factored the same way.

Below, you will find examples for how to solve a quadratic equation by factoring for three different occasions:

when the leading coefficient a=1 (this applies to Example #1)
when the leading coefficient a≠1

For a more in-depth review of factoring trinomials, we highly recommend visiting our popular Step-by-Step Guide to Factoring Polynomials. Otherwise, let’s continue on to learning how to factor quadratic equations when a=1.

How to Factor Quadratic Equations When a=1

For this first section, we will focus on how to factor a quadratic equation with a leading coefficient of 1 (as opposed to any other number). Figure 08 highlights the difference between a quadratic equation where a=1 and a quadratic equation where a≠1.

Example #2: Factor and Solve x² -2x -15 = 0

First, note that this quadratic equation is in the form ax² + bx + c = 0 since the equation could be rewritten as:

x² + (-2x) + (-15) =0

However, for the sake of simplicity, we will keep it as:

x² -2x -15 =0

Since a=1 in this example, we can solve this quadratic equation the same way we solved Example #1.

First, we can split the quadratic into two parts: the left-side of the equal sign and the right-side of the equal sign. Then we can attempt to factor the trinomial x² -2x -15 on the left-side.

Now, we can find the factors of x² -2x -15 as follows:

Step One: Identify the values of b and c.

In this example, the values of b and c are: b=-2 & c=-15

Step Two: Find two numbers that both ADD to b and MULTIPLY to c.

Once you have identified the values of b and c (-2 and -15 respectively in this example), you can use trial-and-error to find two numbers that both add to the b term (-2) and multiply to the c term (-15). Another way to say this is: find two numbers with a sum of -2 and a product of -15.

In cases like this example, you need two number that will multiply to a -15. Since the product of two negatives is always positive and the product of two positives is also always positive, your factors will include one positive number and one negative number.

After some trial-and-error, you will find that 3 and -5 work because:

3 + -5 = -2 (the value of b) ✓
3 x -5 = -15 (the value of c) ✓

Since the sum of 3 and -5 is -2 and the product of 3 and -5 is -15, you have found out that the factors of the trinomial x² -2x -15 are (x+3) and (x-5)

Step Three: Use your numbers from step two to write out the factors

In this case, you can conclude that the factors of x² -2x -15 are (x+3) and (x-5).

From here, we have a new equation to deal with:

(x+3)(x-5)=0

To find the solution(s) to the original quadratic equation, we have to take each factor, set it equal to zero, and solve for x as follows:

x+3 = 0 → x = -3
x-5 = 0 → x = 5

Final Answer: The quadratic equation x² - 2x - 15 =0 has a solution of x={-3,5}.

Now, let’s look at one more example of how to factor quadratic equations when the leading coefficient is 1.

Example #3: Factor and Solve x² + 4x = 12

Do you notice anything different about this next example?

The equation is not a quadratic (i.e. it is not in ax² +bx + c = 0 form). To get this equation into ax² +bx + c = 0, we will have to rearrange it, namely by subtracting 12 from both sides so that there is a zero on the right side of the equals sign as follows:

x² + 4x = 12
x² + 4x -12 = 12 -12
x² + 4x -12 = 0

By rearranging the terms in this way, our new equation is a quadratic that is now in ax² +bx + c = 0 form, meaning that we can solve it by factoring.

Now, we can find the factors of x² +4x -12 as follows:

Step One: Identify the values of b and c.

In this example, the values of b and c are: b=4 & c=-12

Step Two: Find two numbers that both ADD to b and MULTIPLY to c.

Once you have identified the values of b and c (4 and -12 respectively in this example), you can use trial-and-error to find two numbers that both add to the b term (4) and multiply to the c term (-12). Another way to say this is: find two numbers with a sum of 4 and a product of -12.

After some trial-and-error, you will find that 6 and -2 work because:

6 + —2 = 4 (the value of b) ✓
6 x —2 = -12 (the value of c) ✓

Step Three: Use your numbers from step two to write out the factors

In this case, you can conclude that the factors of x² + 4x -12 are (x+6) and (x-2).

Finally, we can find our solutions by solving

(x+6)(x-2)=0

To find the solution(s) to the original quadratic equation, we have to take each factor, set it equal to zero, and solve for x as follows:

x+6 = 0 → x = -6
x-2 = 0 → x = 2

Final Answer: The quadratic equation x² + 4x - 12 = 0 has a solution of x={-6,2}.

The entire step-by-step process for solving this example is illustrated in Figure 12 above. Now let’s move onto learning bow to factor a quadratic equation when the leading coefficient is not equal to one.

How to Factor Quadratic Equations When a≠1

Example #4: Factor and Solve 2x² - x - 6 = 0

For the first example, we have to find the solutions to the quadratic equation: 2x² - x - 6 = 0.

Notice that, in this case, the leading coefficient a≠1 (in this example a=2).

We can still solve this quadratic equation by separating the left and right-side of the equal sign where the trinomial is on the left side and the zero is on the right side as shown in Figure 13 below.

Now, we have to find the factors of the trinomial 2x² - x - 6 on the left-side of the equal sign as follows:

Factoring these types of trinomials is a bit more involved.

First, notice that you can not pull out a greatest common factor (GCF). When this is the case, you can use the AC method for factoring trinomials of the form ax² + bx + c when a≠1 as follows:

Step One: Identify the values of a and c and multiply them together

For this example, a=2 and c=-6…

a x c = 2 x -6 = -12

Step Two: Factor and replace the middle term

Next, you have to take the resulting product from Step One (-12) and use it as a replacement for the middle term.

This means that you are replacing the middle term, -1x, with -12x, which we then have to factor as follows:

-12 = -4 x 3; and
-4 + 3 = -1

We chose -4 and 3 as factors because the sum of -4 and 3 equals negative 1, so we can rewrite the original trinomial as 2x² - 4x +3x - 6, as shown in Figure 15 below.

Step Three: Split the new polynomial down the middle and take the GCF of each side

Our new polynomial is equivalent to the one that we started with, but now it has four terms: 2x² - 4x + 3x - 6

Now, you must split the polynomial down the middle to essentially create two separate binomials that you can simplify by dividing GCF’s out of as follows:

First Binomial: 2x² - 4x = 2x(x-2)
Second Binomial: 3x - 6 = 3(x-2)

This process of splitting the polynomial down the middle is illustrated in Figure 16 below.

Step Four: Identify the Factors

Lastly, you can now determine the factors.

The result from the previous step was 2x(x - 2) + 3(x -2). Within this expression you will find your two factors, (2x+3) and (x-2), as shown in Figure 17 below.

And now, you can conclude that the factors of 2x² - x - 6 are (2x+3) and (x-2).

Unfortunately, you still have to set these factors equal to zero and solve for x to find the solution to the original quadratic equation as follows:

2x + 3 = 0 → 2x = -3 → x = -3/2
x-2 = 0 → x = 2

Final Answer: The quadratic equation 2x² - x - 6 = 0 has a solution of x={ -3/2 , 2 }.

The complete step-by-step process for solving this final example is illustrated in Figure 18 below.

Conclusion: How to Solve Quadratic Equations by Factoring

Learning how to factor quadratic equations is a key algebra skill that can be learned with practice.

While many students will initially learn how to solve quadratic equations by graphing, the next step will be to learn how to solve quadratic equations by factoring, which means that you will have to know how to factor quadratic of the form ax² + bx + c = 0 when a=1 and when a≠1.

In this step-by-step guide to factoring quadratic equations, we covered both cases as we worked through several examples of factoring quadratics of the form ax² + bx + c = 0. Remember that not all questions will be directly in this form, but they can often be rearranged (i.e. they can be rewritten as an equivalent equation that is in the form ax² + bx + c = 0).

If you are still confused about how to factor quadratic equations, we highly recommend that you go back and work through all of the example problems above, carefully following each step. The more experience that you have working on these types of problems, the easier they will become.