How to Find Scale Factor in 3 Easy Steps

Step-by-Step Guide: How to Find the Scale Factor of a Dilation

When learning about geometry transformations on the coordinate plane, dilations can be tricky since they are the only transformation that involves changing the shape of the original figure. In the case of dilating a figure, we use something called scale factor to determine whether to stretch a figure (make it larger) or shrink a figure (make it smaller) as well as by what factor.

This free step-by-step guide on How to Find Scale Factor in 3 Easy Steps will teach you how to determine the scale factor of a given dilation by looking at its graph and/or a given set of coordinate points.

This guide will cover the following topics:

What is a Dilation?
What is Scale Factor?
How to Find Scale Factor Example #1
How to Find Scale Factor Example #2
How to Find Scale Factor Example #3

You can use the quick-links above to skip to any section of this guide. However, if are new to finding the scale factor a dilation, we recommend working through each section in order.

Now, let’s start off with a quick review of dilations and the definition of scale factor.

What is a Dilation?

Before we learn how to find the scale factor of a dilation, it’s important that we understand what a dilation is in the first place.

There are four types of transformations in geometry:

Rotations: When you turn the object clockwise or counter-clockwise about a given point
Reflections: When you create a mirror image of the original shape across a line of symmetry
Translations: When you slide a figure from one location on the coordinate plan to another
Dilations: When you stretch or shrink the image of a figure based on a given scale factor

This guide will focus on the fourth type of transformation—dilations.

Definition: Dilation

In math, a dilation refers to a transformation that results in a figure changing in size, but not shape. This means that the new figure will be made larger or smaller to the original figure, but it will remain proportional.

Figure 02 above illustrates an example of a dilation where the image of ▵ABC is being stretched to form the new larger ▵A’B’C’.

Notice, however, that both triangles have the same shape and are proportional to each other. ▵A’B’C’ is just a scaled up version of ▵ABC.

What is Scale Factor?

Definition: Scale Factor

Every dilation is based on a scale factor, which we will denote using the letter k in this guide.

In math, a scale factor refers to the ratio between the side lengths and coordinate points of two similar figures. In the case of dilations, scale factor is used to describe by what factor the original image has been stretched (enlarged) or shrunk (reduced) in size.

When the scale factor, k, is greater than one, the result is an enlargement. When the scale factor, k, is less than one, the result is a reduction.

Figure 03 illustrates the relationship between an image and its scale factor in terms of the new image being larger or smaller.

Note that the scale factor of a dilation must always be positive (i.e. the scale factor can never be zero or a negative number). Scale factors, however, can be equal to fractions (which we will see more of later on).

The key takeaway here is that the scale factor of a dilation is what tells you if an image is being made larger (stretched) or smaller (shrunk) and by what factor.

Now, let’s take a closer look at the dilation shown in Figure 01 above to see if we can figure out the scale factor in our first example below:

How to Find Scale Factor in 3 Easy Steps

Now that you are familiar with the key concepts and definitions associated with dilations and scale factor, you are ready to learn how to find the scale factor of a dilation using the following simple steps:

Step 01: Determine the coordinates of a point on the original figure and the coordinates of the coordinates of the corresponding point on the new dilated figure.
Step 02: Divide the x-value of the new figure coordinate by the x-value of the original figure coordinate to find the scale factor.
Step 03: Repeat Step 02 using the y-values to confirm your answer.

Are you ready to try out our 3-step method for finding the scale factor of a dilation? Let’s go ahead and apply these steps to solving our first problem.

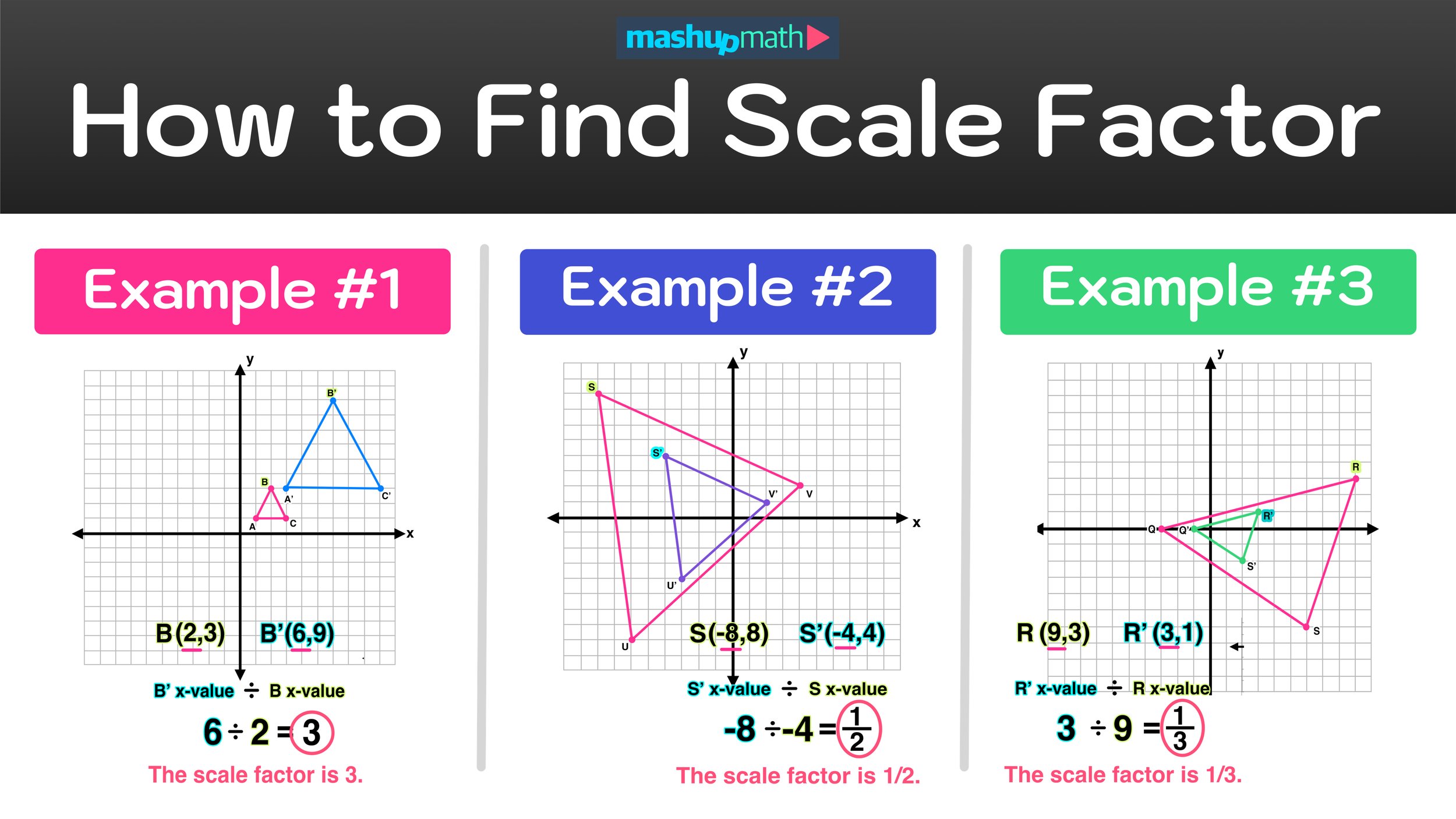
Example #1: How to Find the Scale Factor

For our first example, we have to find the scale factor that was used to dilated ▵ABC onto ▵A’B’C.

For starters, we know than the original image is ▵ABC and the new image is ▵A’B’C’. Notice that the new image is larger than the original image, so we should expect our resulting scale factor to be greater than one.

Let’s go ahead and apply our three steps to see if this is the case:

Step 01: Determine the coordinates of a point on the original figure and the coordinates of the coordinates of the corresponding point on the new dilated figure.

For the first step, we can select any point on the original image, ▵ABC. In this case, let’s select point B with coordinates (2,3). The corresponding point on ▵A’B’C’ is point B’ with coordinates at (6,9).

Original Image Point: B (2,3)
Corresponding Point on New Image: B’ (6,9)

Note that you could have chosen points A and A’ or points C and C’. As long as you are consistent, you will be able to find the scale factor.

Step 02: Divide the x-value of the new figure coordinate by the x-value of the original figure coordinate to find the scale factor.

Next, we have to take the x-value of the point from the new figure (point B’) and divide it by the x-value of the corresponding point on the original figure (point B), as follows:

The x-value of Point B’ at (6,9) is 6
The x-value of Point B at (2,3) is 2
6 ➗ 2 = 3

Now we can conclude that our result is the value of our scale factor, so we can say that:

The scale factor is 3.

When we concluded that the scale factor is 3, we are saying that ▵A’B’C’ is three times as large as ▵ABC.

This should make sense by looking at the graph and by remembering that we were expecting to have a scale factor greater than one in the first place. However, to ensure that we are correct, let’s go ahead and complete the third and final step.

Step 03: Repeat Step 02 using the y-values to confirm your answer.

Finally, we have to take the y-value of the point from the new figure (point B’) and divide it by the y-value of the corresponding point on the original figure (point B), as follows:

The y-value of Point B’ at (6,9) is 9
The y-value of Point B at (2,3) is 3
9 ➗ 3 = 3

We got the same answer! Now, we can conclude that:

Final Answer: The scale factor is 3.

It’s okay if you are still a little confused. Let’s go ahead and work through another example where we will find the scale factor of a dilation using our 3-steps.

Example #2: How to Find the Scale Factor

For this second example, we are again tasked with finding the scale factor of a dilation.

In this example, we can see that the new image of ▵S’U’V’ is the result of shrinking ▵SUV (since ▵S’U’V’ is smaller than ▵SUV). So, we know that our scale factor should be less than one.

We can now use of 3-steps to find the exact scale factor as follows:

Step 01: Determine the coordinates of a point on the original figure and the coordinates of the coordinates of the corresponding point on the new dilated figure.

Again, you can choose any point that you like as long as you are consistent. In this case, let’s choose point S on ▵SUV with coordinates at (-8,8). The corresponding point on ▵S’U’V’ is point S’ with coordinates at (-4,4).

Original Image Point: S (-8,8)
Corresponding Point on New Image: S’ (-4,4)

Step 02: Divide the x-value of the new figure coordinate by the x-value of the original figure coordinate to find the scale factor.

For the next step, let’s take the x-value of the point from the new figure (point S’) and divide it by the x-value of the corresponding point on the original figure (point S), as follows:

The x-value of Point S’ at (-4,4) is -4
The x-value of Point S at (-8,8) is -8
-4 ➗ -8 = 1/2

Now we can conclude that our result is the value of our scale factor, so we can say that:

The scale factor is 1/2.

A scale factor of 1/2 means that the original figure, ▵SUV, was shrunk down to half of its size to create the image of ▵S’U’V’.

Before we can confirm that our answer is correct, however, let’s complete the third and final step.

Step 03: Repeat Step 02 using the y-values to confirm your answer.

For step number three, we must take the y-value of the point from the new figure (point S’) and divide it by the y-value of the corresponding point on the original figure (point S), as follows:

The y-value of Point S’ at (-4,4) is 4
The y-value of Point S at (-8,8) is 8
4 ➗ 8 = 1/2

Notice that our result, again, is 1/2, so we can say that:

Final Answer: The scale factor is 1/2.

Are you starting to get the hang of it? Let’s go ahead to work through another example.

Example #3: How to Find the Scale Factor

Let’s go ahead and use our 3-step method to solve this final example.

We can use the same 3-step method that we did on the previous two examples to solve this problem.

Notice that the new image of ▵Q’R’S’ is the result of shrinking the original image of ▵QRS, so our scale factor should be less than one.

Step 01: Determine the coordinates of a point on the original figure and the coordinates of the coordinates of the corresponding point on the new dilated figure.

Just like the last two examples, you can choose any point that you like as long as you are consistent. However, for this problem, we will intentionally avoid points Q and Q’ since they both have zero as coordinate points, which could cause problems since we can’t have zero in a denominator.

Instead, let’s choose point R on ▵QRS with coordinates at (9,3). The corresponding point on ▵Q’R’S’ is point R’ with coordinates at (3,1).

Original Image Point: R (9,3)
Corresponding Point on New Image: R’ (3,1)

Step 02: Divide the x-value of the new figure coordinate by the x-value of the original figure coordinate to find the scale factor.

Moving on, we have to take the x-value of the point from the new figure (point R’) and divide it by the x-value of the corresponding point on the original figure (point R), as follows:

The x-value of Point R’ at (3,1) is 3
The x-value of Point R at (9,3) is 9
9 ➗ 3 = 1/3

So, we have just figured out the ▵QRS was shrunk by a scaled factor of 1/3 to get the image of ▵Q’R’S’.

The scale factor is 1/3.

In other words, ▵Q’R’S’ is one-third the size of ▵QRS.

All that we have to do now is confirm that our answer is correcting by completing the third step.

Step 03: Repeat Step 02 using the y-values to confirm your answer.

To confirm that the scale factor was 1/3 is correct, we have to take the y-value of the point from the new figure (point R’) and divide it by the y-value of the corresponding point on the original figure (point R), as follows:

The y-value of Point R’ at (3,1) is 1
The y-value of Point R at (9,3) is 3
1 ➗ 3 = 1/3

Now that our answer has been confirmed, we can make the following conclusion:

Final Answer: The scale factor is 1/3.

Conclusion: How to Find Scale Factor

Understanding how to determine the scale factor of a dilation is an important geometry and algebra skill that every student must master when they are learning about transformations on the coordinate plane.

This step-by-step guide of finding scale factor reviewed the definition of a dilation on the coordinate plane and the meaning of scale factor in regards to dilations. When a scale factor, k, is greater than one, the resulting image is larger than the original image. And, when the scale factor, k, is less than one, the resulting images is smaller than the original image.

To solve problems where you are tasked with finding the scale factor of a dilation, we applied the following three step strategy:

Step 01: Determine the coordinates of a point on the original figure and the coordinates of the coordinates of the corresponding point on the new dilated figure.

Step 02: Divide the x-value of the new figure coordinate by the x-value of the original figure coordinate to find the scale factor.
Step 03: Repeat Step 02 using the y-values to confirm your answer.

You can use these three steps to solve any problem where you are tasked with finding the scale factor of a dilation between two figures on the coordinate plane.